DECO Research Series #4: Hiding Secret Lengths
Author: Siam Hussain
Contributors: Dahlia Malkhi, Jasleen Malvai, Gregory Neven, Alexandru Topliceanu, Xiao Wang, Fan Zhang
In the previous post, we discussed how to parse a JSON response received from a server without revealing the values of the sensitive data within the response. In this post, we discuss how to additionally hide the individual lengths of sensitive data from the verifier.
In the commit-and-prove ZKP used in DECO, where the prover commits individually to every bit of the secret input, the verifier learns the lengths of the prover’s private inputs. In fact the majority of the ZKP protocols in general, both interactive and non-interactive, reveal the lengths of the prover’s private inputs. In many scenarios, lengths may leak significant information about sensitive data. For example, if the account balance of the prover has 6 digits, we know that the prover has at least hundred thousand dollars in her account.
We now describe how DECO allows the prover to pad the JSON scalars to hide their individual lengths while still being able to prove that she did not modify the value of any of these scalars from what was received from the server.
Quick Recap
We begin with a quick recap of the relevant concepts from the last two posts in this series. In the second post, we described how the prover proves that a JSON response $R$ is received from a particular server. At the end of that post, the prover and the verifier hold a commitment $[R]$ to the authenticated response.
In the third post of this series, we described how the prover helps the verifier to efficiently parse the JSON response while preserving privacy of the sensitive scalar values within the JSON. The prover sends two pieces of information to the verifier: (i) a redacted JSON $R’$, which has all the JSON scalar values from $R$ redacted, and (ii) a commitment $[Z]$ to the array of scalars $Z$. To ensure that $R’$ and $Z$ are computed correctly from $R$, the verifier performs a series of checks. Among them, check 1 ensures that replacing all the redacted values in $R’$ with the corresponding values from $Z$ results in $R$. In this check, the prover and the verifier locally computes an array of split string $P$ by splitting $R’$ at the location of scalars and verifies the following reconstruction statement through ZKP. Here, $m$ denotes the number of scalars.
$\big[ R \big] =? \big[ P[0] \| Z[0] \| P[1] \| Z[1] \| \cdots \| P[m-1] \| Z[m-1] \| P[m] \big]$
In this post, we illustrate this statement with the following example JSON response $R$ representing the financial report of the prover.
{
"name" : "Alice Liddell",
"ssn" : "012-345-6789",
"date_generated": "05-16-2023",
"accounts": [
{
"balance": 12345,
"account_id": 156461324651
},
{
"balance": 1000000,
"account_id": 213612867132,
},
{
"balance": 2000000,
"account_id": 371823713701
}
]
}
The array of scalars, $Z$ for this JSON response is the following.
[
"\"Alice Liddell\"",
"\"012-345-6789\"",
"\"05-16-2023\"",
"12345",
"156461324651"
"1000000",
"213612867132",
"2000000",
"371823713701"
]
In the commitment scheme used in DECO, the prover commits to every bit in $Z[i]; i = 0, \cdots, m-1$ individually. This reveals the length of every element of $Z$ which may leak information about their values. For instance, by observing $\big[Z[3]\big]$, the verifier knows that the prover has at least $10000 in her first account since it has 5 digits in the balance.
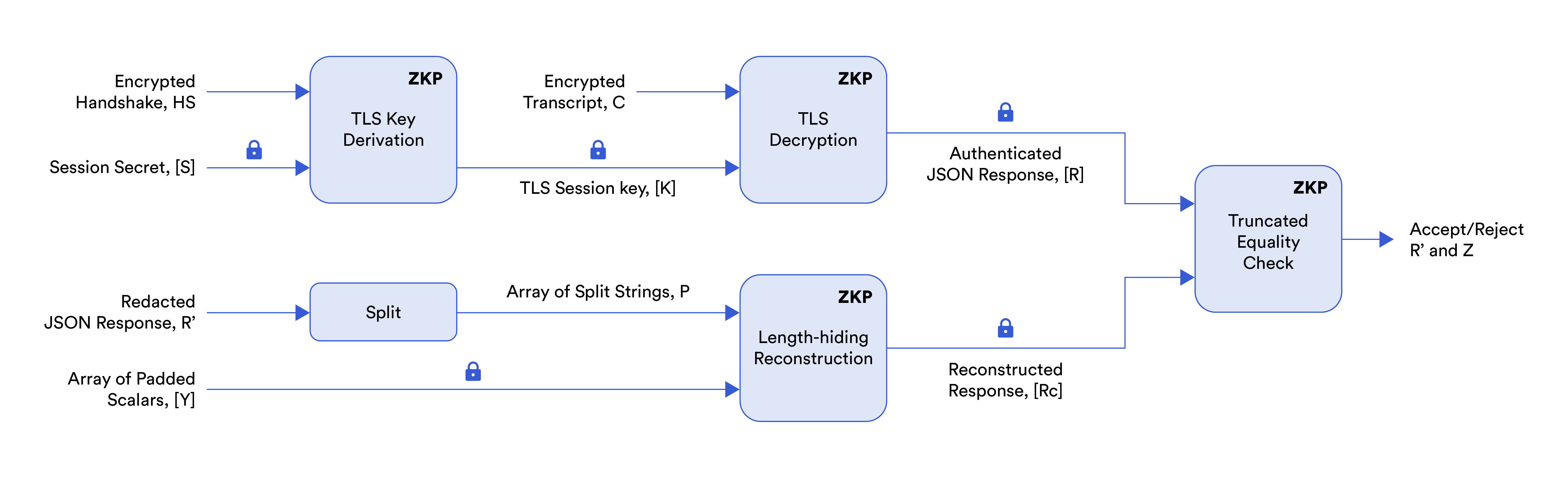
The above figure illustrates the steps of the DECO protocol as explained in this post. The arrows marked with the lock icon indicate private inputs known only to the prover and $[x]$ denotes commitment to a private input $x$. The other inputs are known to both the prover and the verifier. In blog 2, we discussed TLS key derivation and TLS decryption. In blog 3, we discussed reconstruction. In this blog, we replace the reconstruction circuit with the length-hiding reconstruction circuit introduced later in this post.
Introducing Padding
In most web applications, servers have upper bounds on various user values. For example, a server could require that a user’s first name be no longer than 30 characters. Or, it may be known that no users have more than $999,999,999,999 (i.e. $1 trillion – $1) in their accounts. However, when such values are scalars in a JSON being used in DECO, their actual lengths may be revealed. We would like to pad inputs to a length that corresponds to such known upper bounds. In the following exposition, we assume that the upper bound on the length of each redacted scaler is agreed upon by the prover and verifier ahead of time.
DECO hides individual lengths by padding each scalar to a constant length. In this length-hiding scheme, instead of committing to the array of scalars $Z$, the prover commits to an array $Y$ of pairs. Each element $Y[i]; i = 0, \cdots, m-1$ in $Y$ is a pair of values: $Z'[i]$, which is $Z[i]$ padded to a known length $H[i]$, and $G[i]$, which is the actual length of $Z[i]$ known only to the prover. For each value of $i = 0, \cdots, m-1$, the prover commits individually to $Z'[i]$ and $G[i]$.
Here is an example of $Y$ which is obtained by padding the example $Z$ shown above. Note that even though we use 0s as padding in this example, they can be any arbitrary characters.
[
( "\"Alice Liddell\"000000000", 15 ),
( "\"012-345-6789\"0000000000", 14 ),
( "\"05-16-2023\"000000", 12 ),
( "12345000000000000000000000000000", 5 ),
( "1564613246510000", 12 ),
( "1000000000000000000000000000000", 7 ),
( "2136128671320000", 12 ),
( "20000000000000000000000000000000", 7 ),
( "3718237137010000", 12 )
]
Length-Hiding Reconstruction Statement
In the reconstruction statement introduced in the third post of this series, the bitwise concatenation (denoted by $\|$) is performed simply by concatenating the commitments to these bits. Now that the prover commits to the array of padded values $Y$ instead of $Z$, the reconstruction statement needs modifications to take care of the padding. If we simply replace $Z[i]$ in the above statement with $Z'[i]$, the equality check will fail since all the padded values will be distributed over the reconstructed string.
We design a length-hiding reconstruction circuit where all the paddings are grouped together at the rightmost locations of the resulting string. The core of this circuit is a length-hiding concatenation sub-circuit (denoted by $\mathbin{\!/\mkern-5mu/\!}$) that groups all the paddings and shifts them to the right, as illustrated in the example below:
$( abc00, 3 ) \mathbin{\!/\mkern-5mu/\!} ( pqrs000, 4 ) \mathbin{\!/\mkern-5mu/\!} ( xyz0000, 3 ) \\
= ( abcpqrs00000, 7 ) \mathbin{\!/\mkern-5mu/\!} ( xyz0000, 3 ) \\
= ( abcpqrsxyz000000000, 10 )$
With this concatenation circuit, the length-hiding reconstruction statement is as follows.
$\big[ R \big] =? \big[ P[0] \mathbin{\!/\mkern-5mu/\!} Y[0] \mathbin{\!/\mkern-5mu/\!} P[1] \mathbin{\!/\mkern-5mu/\!} Y[1] \mathbin{\!/\mkern-5mu/\!} \cdots \mathbin{\!/\mkern-5mu/\!} P[m-1] \mathbin{\!/\mkern-5mu/\!} Y[m-1] \mathbin{\!/\mkern-5mu/\!} P[m] \big]$
Since the right-hand side of the equality check is longer than the left due to the padding, the reconstructed string on the right is truncated up to the length of $R$. Both prover and verifier know the length of the response $R$ since it corresponds to the length of the TLS ciphertext $C$.
For the above example, the right-hand side after the reconstruction is as follows:
"{\n \"name\" : \"Alice Liddell\",\n \"ssn\" : \"012-345-6789\",\n \"date_generated\": \"05-16-2023\",\n \"accounts\": [\n {\n \"balance\": 12345,\n \"account_id\": 156461324651 \n },\n {\n \"balance\": 1000000,\n \"account_id\": 213612867132 \n },\n {\n \"balance\": 2000000,\n \"account_id\": 371823713701 \n }\n ]\n}000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000"
Security Argument
In the previous post, we discussed a series of soundness checks performed by the verifier to ensure the correctness of parsing. In this post, we have presented a modification to check 1 to enable hiding the lengths of sensitive scalar values in the JSON response. We now analyze the security of the modified system.
The prover now commits to two new pieces of data: the padding characters and the actual lengths of the scalars. The values used in the padding characters are inconsequential to the new reconstruction statement since the equality check is performed only up to the length of $R$, ignoring the padding characters at the rightmost location of the reconstructed string. For the values of the actual length of the scalars, prover can deviate from the honest behavior in two ways — she commits to a value either smaller or larger than the actual length. Let us examine these two cases.
If the prover commits to a smaller value, the characters at the end of the corresponding scalar will be moved to the rightmost locations. As a result, the reconstructed string will no longer match with the authenticated TLS response $R$. In the above example, if the prover commits to `( “12345000000000000000000000000000”, 2)` (the actual length is 5) for the fourth element of $Y$, the resulting reconstructed string will be as follows, which does not match with the original response received from the server. Therefore, the reconstruction statement will evaluate to $\texttt{false}$.
"{\n \"name\" : \"Alice Liddell\",\n \"ssn\" : \"012-345-6789\",\n \"date_generated\": \"05-16-2023\",\n \"accounts\": [\n {\n \"balance\": 12,\n \"account_id\": 156461324651 \n },\n {\n \"balance\": 1000000,\n \"account_id\": 213612867132 \n },\n {\n \"balance\": 2000000,\n \"account_id\": 371823713701 \n }\n ]\n}3450000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000"
If the prover commits to a larger value of the actual length, some of the padding characters will remain in the middle of the reconstructed string instead of being moved to the rightmost location. This will again cause the reconstruction statement to evaluate to $\texttt{false}$. In the above example, if the prover commits to `( “12345000000000000000000000000000”, 10)` (the actual length is 5) for the fourth element of $Y$, the resulting reconstructed string will be as follows. The extra `0` at the end of the "balance" field will cause a mismatch with the original response.
"{\n \"name\" : \"Alice Liddell\",\n \"ssn\" : \"012-345-6789\",\n \"date_generated\": \"05-16-2023\",\n \"accounts\": [\n {\n \"balance\": 1234500000,\n \"account_id\": 156461324651 \n },\n {\n \"balance\": 1000000,\n \"account_id\": 213612867132 \n },\n {\n \"balance\": 2000000,\n \"account_id\": 371823713701 \n }\n ]\n}00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000"
Length-Hiding Concatenation Circuit
So far we have described what the length hiding concatenation does. We now present how it works. The building block of the length-hiding concatenation circuit is an oblivious left shift sub-circuit; it proves that an $n$-character string $v$ is obtained by shifting an $n$-character string $u$ by $l$ characters without revealing any of $u$, $v$, or $l$. The number of AND gates in this circuit is $8n$ (assuming each character is 1 byte = 8 bits). Recall that the cost of the ZKP execution depends on the number of AND gates in the circuit. We omit the details of the sub-circuit in this blog and refer interested readers to [FJLO+21].
We now present the concatenation circuit for padded inputs $u_l$, $u_r$ with actual lengths $g_l$, $g_r$ and padded lengths $h_l$, $h_r$, respectively. The output of the circuit is $v$ with actual length $g_l + g_r$ and padded length $h_l + h_r$. Verifier only knows $h_l$ and $h_r$. Specifically,
$( u_l, g_l ) \mathbin{\!/\mkern-5mu/\!} ( u_r, g_r )\,=\,( v, g_l + g_r )$.
The computations performed in the circuit are shown below. Here, $zeros(z)$ returns a string with $z$ zeros, $\oplus$ denotes bitwise XOR. We illustrate the computations with the following example: $u_l = abc00, u_r = pqrs000$; $g_l = 3, g_r = 4$; $h_l = 5, h_r = 7$.
| Step | Operation | Example |
| 1 | $v_0 = zeros(h_l) \| u_r$ | $v_0 =$ $00000pqrs000$ |
| 2 | $v_1 = v_0 \ll (h_l – g_l)$ | $v_1 =$ $000pqrs00000$ |
| 3 | $v_2 = u_l \| zeros(h_r)$ | $v_2 =$ $abc000000000$ |
| 4 | $v = v_1 \oplus v_2$ | $v =$ $abcpqrs00000$ |
The only costly operation in the concatenation circuit is step 2. The number of AND gates in this step is $\mathcal{O}(h_l + h_r)$, which is the padded length of $v_1$ as well as the final result $v$. Therefore, when performing a series of concatenations to compute the right-hand side of the length-hiding reconstruction statement, we should keep the length of the intermediate results short. The total cost depends on the sequence in which we perform these concatenations. In the following we show two possible sequences, $A$ and $B$.
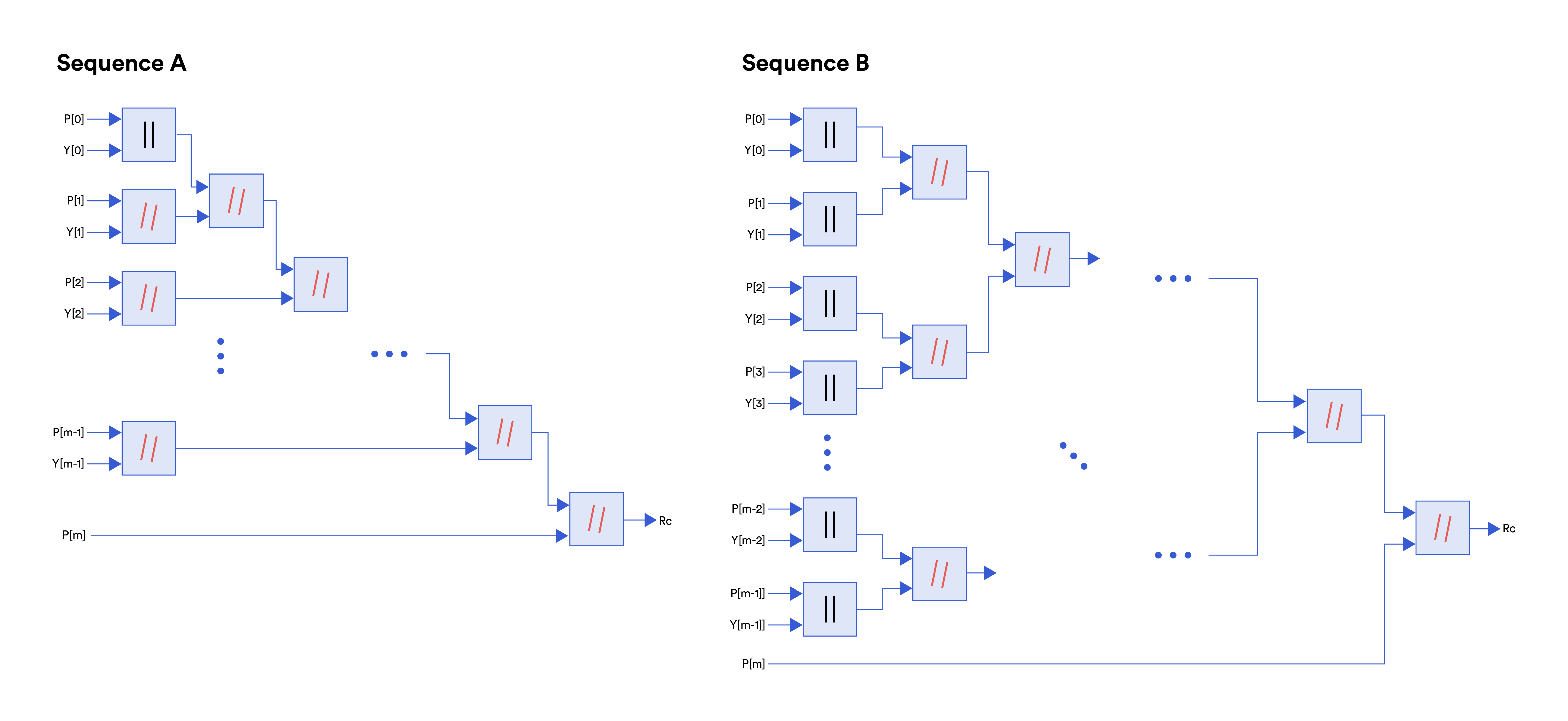
Now let’s have a look at the operations of these two possible designs of the reconstruction circuit and the cost of evaluating them through the interactive ZKP protocol.
Sequence $A$:
1. Initialize $R_c = P[0] \| Y[0]$
2. For $i = 1 \cdots m-1$
$R_c = R_c \mathbin{\!/\mkern-5mu/\!} P[i] \mathbin{\!/\mkern-5mu/\!} Y[i]$
3. $R_c = R_c \mathbin{\!/\mkern-5mu/\!} P[m]$
Sequence $B$:
For simplicity, let’s assume $m = 2^d$.
1. Initialize $PY$ as an array of $m$ strings
2. For $i = 0 \cdots m-1$
$PY[i] = P[i] \| Y[i]$
3. For $j = d-1 \cdots 0$
For $i = 0 \cdots 2^j-1$
$PY[i] = PY[2*i] \mathbin{\!/\mkern-5mu/\!} PY[2*i+1]$
4. $R_c = PY[0] \mathbin{\!/\mkern-5mu/\!} PY[m]$
In sequence $A$, we keep concatenating to one intermediate string, the length of which keeps increasing, thus increasing the total cost. In sequence $B$, we form multiple shorter intermediate strings by concatenating the strings in pairs. Note that the first concatenation between one element in $Z’$ to the right of one element in $P$ is just simple bitwise concatenation since $P$ does not have secret paddings.
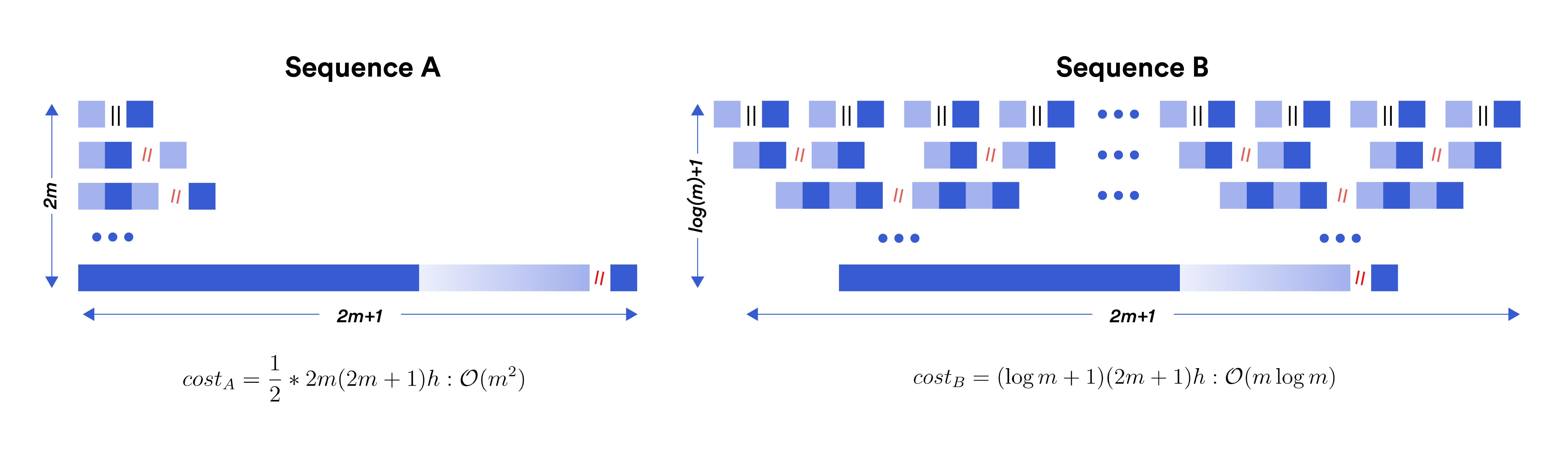
In the above figure, we illustrate how the number of AND gates stack up in the two sequences $A$ and $B$. The actual data and padding are shown in dark and light shades, respectively. For simplicity, we assume each element in $P$ and $Z’$ have the same length $h$. The cost of each concatenation ($\mathbin{\!/\mkern-5mu/\!}$) is the sum of the lengths of the left- and right-hand sides.
Sequence $A$: There is a single concatenation in each step with increasing output length. We can view this as a triangle, the area of which represents the total number of AND gates. Thus the number of AND gates in this sequence, $cost_A \approx \frac{1}{2} \times 8(2m+1)h(2m)$, which has a complexity of $\mathcal{O}(m^2)$.
Sequence $B$: There are multiple concatenations in each step. As the length of the output increases, the number of concatenations decreases, making the total cost at each step a constant. Thus it resembles a rectangle with much shorter height compared to the triangle. The number of AND gates in this sequence is $cost_B \approx 8(2m+1)h \log m$, which has a complexity of $\mathcal{O}(m \log m)$.
Thus sequence $B$ provides more efficient computation compared to sequence $A$.
Selective Redaction of Scalars
Before concluding this post, we present an optimization supported in DECO. The cost of length-hiding reconstruction is $\mathcal{O}(m \log m)$ where $m$ is the number of scalars. This cost is incurred in order to hide the length of the scalars. To achieve more efficient computation, the prover may choose not to hide the lengths of a selected set of scalars. For instance, in the example JSON response used in this post, prover may be willing to reveal the length of the "account_id" field to achieve more efficient computation.
The current implementation of DECO takes this one step further by providing the option to the prover to reveal not only the lengths but also the values of a selected set of non-sensitive scalars. It allows the verifier to attest to some metadata present in the received response. In the example JSON response, the prover may choose to reveal the "date_generated" field. This field is not specific to the individual prover and thus does not reveal any sensitive information. However, revealing this allows the verifier to attest to the date on which the inputs to the claims were valid.
This is the fourth post in a series of DECO research blogs from the Chainlink Labs Research Team. Check out the other posts in the series:
- DECO Research Series #1: An Introduction
- DECO Research Series #2: Provenance and Authenticity
- DECO Research Series #3: Parsing the Response
References
[FJLO+21] Nicholas Franzese, Jonathan Katz, Steve Lu, Rafail Ostrovsky, Xiao Wang, and Chenkai Weng. “Constant-Overhead Zero-Knowledge for RAM Programs.” In ACM Computer and Communications Security 2021.
