DECO Research Series #3: Parsing the Response
Author: Siam Hussain
Contributors: Lorenz Breidenbach, Dahlia Malkhi, Alexandru Topliceanu, Xiao Wang, Chenkai Weng, Fan Zhang
In the previous post, we described how the authenticity of the TLS response is verified. In this post, we discuss how to efficiently and reliably parse the response and form claims about it while preserving the privacy of sensitive data within the response.
At the end of the last post, the prover and the verifier held commitment $[R]$ to the authenticated TLS response. The response $R$ is an array of bytes or a string. DECO then enables the prover to convince the verifier that some claim about $R$ is true without leaking sensitive information in $R$. For example, if $R$ is the following JSON document representing the financial report of the prover, she may claim that her bank balance is above $1,000,000 without revealing the exact balance.
{
"balance": 2000000,
"account_id": 156461324651,
}
Since the verifier does not see $R$ in plaintext, this creates a security challenge: how to prove that the value about which the claim is made is extracted from the correct context. To be specific, how could the verifier be sure that the proof is about the “balance” field as opposed to “account_id”. This issue might seem trivial at first glance, since JSON can be parsed in unambiguously. However, the problem is that parsing JSON in ZKP would be prohibitively expensive.
In this post, we discuss efficient ways to parse the claim and prove the correctness of parsing. Specifically, we present a protocol to extract commitments to particular fields from the commitment to a string. While we focus on JSON, one of the most widely used grammars in API responses, the concepts discussed here also apply to related grammars like XML or YAML.
Challenges in Parsing JSON in ZKP
While parsing a JSON in plaintext is pretty straightforward, it is extremely expensive in ZKP, where the structure of the JSON is hidden from the verifier. To explain this, let us start with a simpler example—the following if-else condition on a secret Boolean $b$.
if (b)
y = f1(x)
else
y = f2(x)
Since $b$ is a secret, the verifier does not know which branch to take. Therefore, both $f1()$ and $f2()$ need to be evaluated through the ZKP protocol, and then the value of $y$ is chosen with a multiplexer circuit.
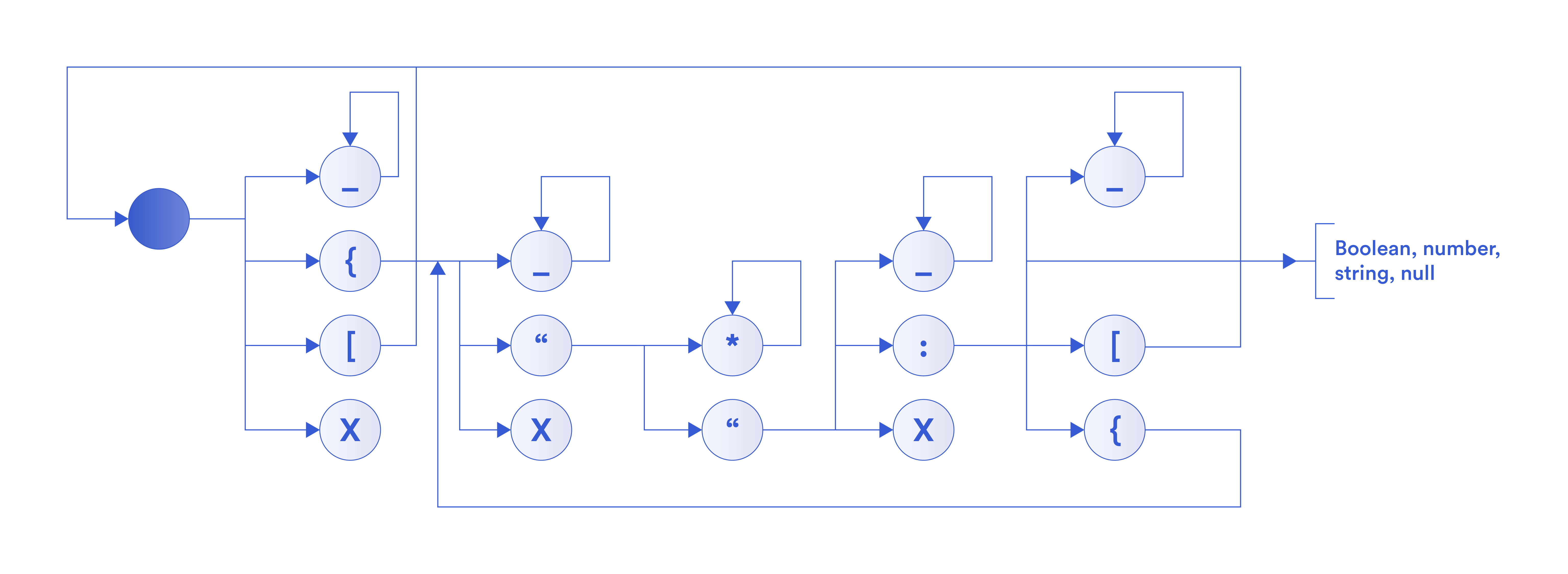
More generally, in the above figure, we show a flow diagram of parsing a JSON document. Starting from the gray node, there are a number of possible branches from each node. Since the verifier does not have access to the JSON document in plaintext, he does not know which branch to take. Therefore, the parser needs to traverse every possible branch. This way, the total number of branches increases exponentially with each character in the string. As a result, a ZKP circuit to parse a JSON document would be too large to handle.
Selective Opening
In practice, however, the structure of the JSON rarely carries any sensitive information. Responses returned by web APIs have similar structures for different users, while the sensitive data items related to a specific user are (typically) the scalar JSON values. In DECO, the prover helps the verifier parse the JSON by partially opening the response to the verifier such that he learns the structure but not the scalars. This enables the verifier to parse the response locally without going through ZKP. At a high level,
- A claim is expressed with a JSON query $q$ in the form $\mathcal{F}(eval(R, q))$ where $eval(R, q)$ denotes the result of applying the query $q$ on $R$ and $\mathcal{F}$ is a function that returns either $\texttt{true}$ or $\texttt{false}$.
- The prover computes (i) a redacted JSON response $R’$ that completely captures the structure of the JSON but has all the scalar values redacted and (ii) an array $Z$ of all the scalars from the JSON. She then sends $R’$ and commitment $[Z]$ to the array $Z$ to the verifier.
- Both parties locally compute an array of indices $J$ in $Z$ such that $Z[J] = eval(R, q)$. Since $R’$ captures the structure of the JSON, the verifier can use it to compute the index of any scalar in $Z$.Finally, they evaluate $\mathcal{F}(Z[J])$ through ZKP on the commitment of the array $Z$.
We illustrate the process with the following toy JSON representing the financial report of the prover. The prover claims that she does not have a negative balance in any of her accounts. Using the jq (a JSON query language) syntax, $q = \texttt{“.accounts[].balance”}$ and $F(x)$ is $min(x) > 0$.
{
"accounts":[
{
"balance": 12345,
"account_id": 156461324651,
},
{
"balance": 1000000,
"account_id": 213612867132,
},
{
"balance": 2000000,
"account_id": 371823713701,
}
]
}
An honest prover sends the following redacted JSON $R’$ to the verifier.
{
"accounts":[
{
"balance": "",
"account_id": "",
},
{
"balance": "",
"account_id": "",
},
{
"balance": "",
"account_id": "",
}
]
}
And commits to the following array of scalars $Z$.
[
"12345",
"156461324651",
"1000000",
"213612867132",
"2000000",
"371823713701"
]
The prover and the verifier both locally compute the array of indices as $J = [0, 2, 4]$. Then they evaluate through ZKP the function $min(Z[J]) > 0$ which returns $\texttt{true}$ since $Z[[0, 2, 4]] = [12345, 1000000, 2000000]$, the minimum of which is $12345$, a positive number.
Soundness Checks
Since the verifier relies on the prover to open the response, he also needs to ensure that the prover opened it properly. The verifier does this through a series of four checks as described below.
Check 0
First, the verifier checks if $R’$ is indeed a valid JSON. He does this by parsing $R’$ using an off the shelf JSON parser. Note that here the verifier is relying on the correct implementation of the parser.
Check 1
Next, the verifier checks if the committed values in the array indeed come from the response. For this, both parties locally compute an array of split strings $P$ by splitting the redacted JSON $R’$ at the location of the scalars and removing the scalars themselves.
For the above example, $P$ is as follows.
[
"{\n \"accounts\":[\n {\n \"balance\": ",
",\n \"account_id\": ",
",\n },\n {\n \"balance\": ",
",\n \"account_id\": ",
",\n },\n {\n \"balance\": ",
",\n \"account_id\": ",
",\n }\n ]\n}"
]
Recall that the parties already hold commitment $[R]$ to the authenticated response. They now use the commitments $[R]$ and $[Z]$ to evaluate the following reconstruction statement in ZK. $m$ here is the number of scalars, $\|$ denotes bit-wise concatenation.
$\big[ R \big] = ? \big[ P[0] \| Z[0] \| P[1] \| Z[1] \| \cdots \| P[m-1] \| Z[m-1] \| P[m] \big]$
The commitment scheme used in DECO commits to every bit in $R$ and $Z[i]; i = 0, \cdots, m-1$ individually. This allows performing the concatenations ($\|$) by simply concatenating the committed bits. The only ZKP operation in this step is the bit-by-bit comparison of the left- and right-hand sides. If the prover alters any value in $Z$, this equality check fails.
Check 2
Now the verifier checks if the redacted response $R’$ completely captures the structure of the response $R$. Before presenting how this check works, let us look at an example of how a dishonest prover may cheat by hiding parts of the structure.
Let’s consider a scenario where the balance in the second account is actually negative, i.e., the received JSON response $R$ is as follows.
{
"accounts": [
{
"balance": 12345,
"account_id": 156461324651,
},
{
"balance": -1000000,
"account_id": 213612867132,
},
{
"balance": 2000000,
"account_id": 371823713701,
}
]
}
The dishonest prover may send the following redacted response and array of scalars to the verifier.
{
"accounts":[
{
"balance": "",
"account_id": "",
},
{
"balance": "",
"account_id": "",
}
]
}
[
"12345",
"156461324651,\n },\n {\n \"balance\": -1000000,\n \"account_id\": 213612867132",
"2000000",
"371823713701"
]
Notice that the prover did not modify any value from $R$. Instead, she rearranged values between $R’$ and $Z$ such that in the view of the verifier, the value of the first “account_id” is the entire highlighter text in the following figure instead of just $156461324651$.

Therefore, these $R’$ and $Z$ will still pass check 1 (you can verify this by computing $P$ for this new $R’$ and interleaving it with the new $Z$). However, $J$ is now $[0, 2]$ and $Z[[0, 2]]$ is [12345, 2000000], minimum of which is greater than 0. With this trick, the prover makes the ZKP evaluation to return $\texttt{true}$ instead of $\texttt{false}$.
To ensure that $R’$ completely captures the structure of $R$, the verifier needs to ensure that the prover is not hiding any part of the JSON structure in $Z$ (i.e., she is not hiding any character that JSON grammar relies on). He achieves this by parsing every element in $Z$ as a scalar through ZKP. JSON supports four types of scalars: number, Boolean, string, and null. If for any element of $[Z]$ parsing as one of these scalars fails, the verifier rejects the claim. In the above example, parsing $Z[1]$ as a scalar will fail since it is not a valid Boolean, number or string. Note that parsing as a scalar does not have the branching issue discussed earlier since the presence of any branch results in an invalid scalar.
Check 3
The final check ensures that $R’$ has all the scalar values redacted. Similar to the previous one, we present an example of how the prover can cheat in the absence of this check. The dishonest prover may send the following redacted response and array of scalars to the verifier.
{
"accounts":[
{
"balance": "",
"account_id": "",
},
{
"balance": -1000000,
"account_id": "",
},
{
"balance": "",
"account_id": "",
}
]
}
[
"12345",
"156461324651",
"213612867132",
"2000000",
"371823713701"
]
Here $J = [0, 2, 4]$. However, the prover reveals one of the scalars to make $Z[[0, 2, 4]] = [12345, 213612867132, 371823713701]$, the minimum of which is greater than 0. Note that this would result in incorrect values of the array $P$ in check 1, resulting in that check failing. However, the verifier can catch this even before starting the ZKP protocol. He computes $R’_v$ by redacting the scalars from $R’$. If the prover indeed redacts all scalars in $R’$, $R’$, and $R’_v$ will be identical. If not, they will be different and the verifier rejects the claim even before starting the ZKP evaluations.
In summary, prover sends a redacted JSON response $R’$ and commitment $[Z]$ to the array of all scalars $Z$ to the verifier such that $R’$ completely captures the structure of the original response $R$. The verifier then verifies the following:
- Replacing all the redacted values in $R’$ with the corresponding values from $Z$ results in the already authenticated response $R$.
- Prover did not redact anything other than the scalars in $R’$.
- Prover did not leave any unredacted scalar in $R’$.
Check 1 ensures the authenticity of the committed scalars. Check 2 and 3 ensure that $R’$ completely captures the structure of $R$, which in turn ensures correct evaluation of JSON queries.
This is the third post in a series of DECO research blogs from the Chainlink Labs Research Team. Check out the other posts in the series:
