DECO Research Series #2: Provenance and Authenticity
Author: Siam Hussain
Contributors: Lorenz Breidenbach, Dahlia Malkhi, Alexandru Topliceanu, Xiao Wang, Chenkai Weng, Fan Zhang
In this post, we describe how the prover convinces the verifier that a TLS response is obtained from a particular server.
DECO involves three parties: the prover (Alice, “she”), the verifier (Bob, “he”), and the TLS server (Charlie, “it”). In TLS, authentication of the server relies on secret challenges generated by the client (prover in DECO) for every new session. This makes TLS an interactive protocol. Therefore, the verifier needs to be a part of the protocol execution to be able to verify the authenticity of data. He achieves this by working as a proxy between the prover and the server and recording the bytes communicated as part of the TLS protocol. These bytes are later used as the “truth” known by both prover and verifier in the proofs of authenticity. Note that TLS ensures the privacy of data from any eavesdropper, in this case the verifier.
The server is oblivious to its participation in the DECO protocol. This requires the TLS protocol to be executed without any modification, and DECO thus follows steps in the TLS protocol precisely. First, the TLS session keys are generated by the prover. Then the keys are used to decrypt the TLS ciphertext.
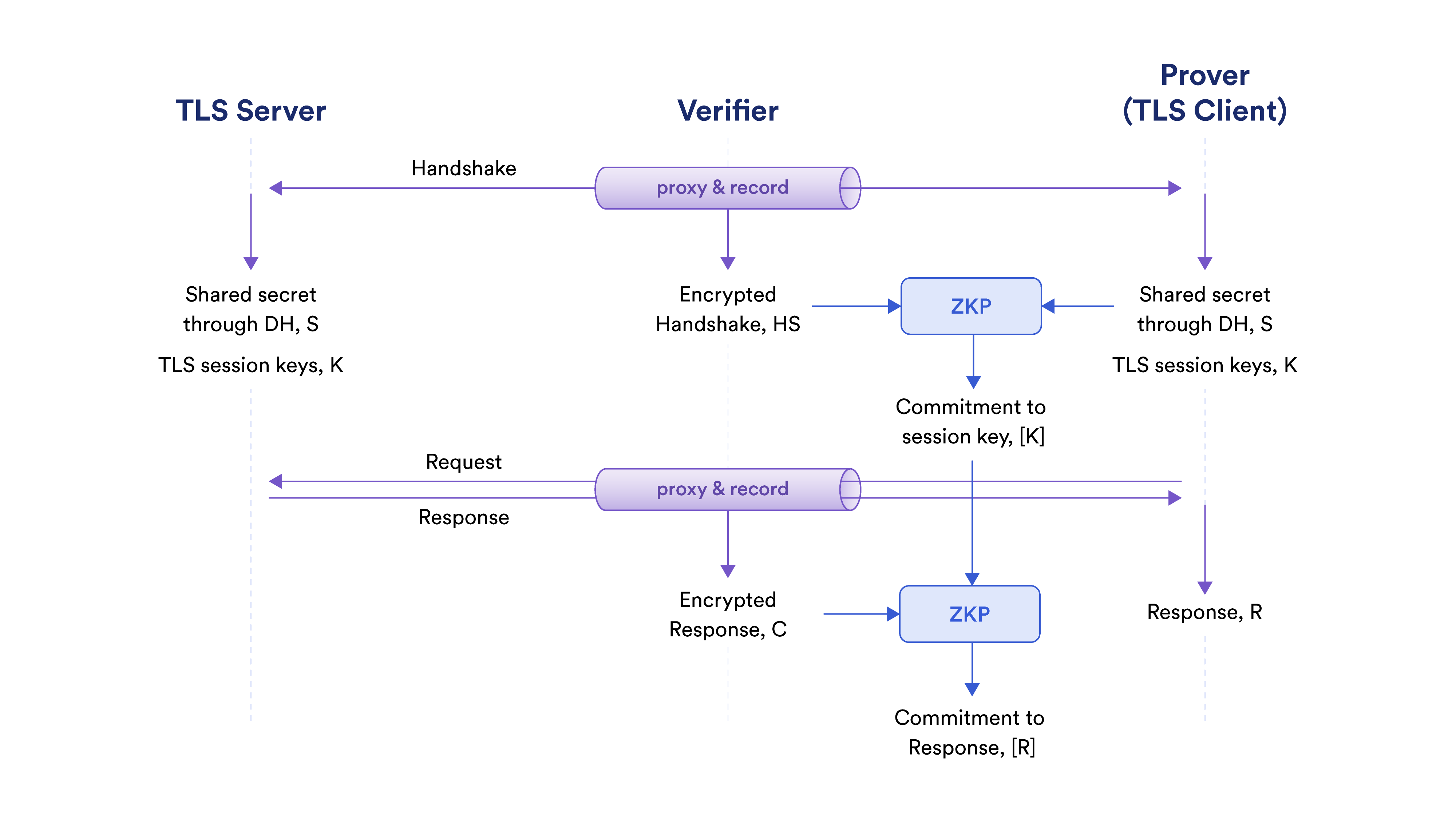
TLS Key Agreement and Key Binding Proofs
At the beginning of the TLS protocol, the prover and server generate a TLS session key $K$ using a key exchange protocol, e.g., Diffie–Hellman. The verifier does not learn $K$ (otherwise TLS wouldn’t be secure). However, this creates a security problem — what if the prover later uses a bogus key $K’$ in the subsequent ZKP proofs? This is possible because encryption algorithms in modern TLS are not committing, which means that a ciphertext can be decrypted in multiple ways. This may allow the prover to decrypt the ciphertext to something the server has never sent, causing a soundness violation. The solution in DECO is to ask the prover to show a key binding proof to prove that the commitment $[K]$ to the session key is generated correctly.
The goal of a key binding proof is for the prover to convince the verifier that a session key $K$ is uniquely bound to the session recorded by the verifier. To understand how key binding proofs work, we first need to cover how TLS session keys are generated.
We use a simplified version of TLS 1.3 inspired by [GZBW22] to illustrate the key ideas. (For clarity, we omit certificate verification and we use $K$ to denote multiple keys.) First, the prover and server generate a shared secret (hidden from the verifier) $S$. Then they locally compute the key $K$ based on $S$. In the following protocol, HMAC is a Hash-Based Message Authentication Code, HKDF is HMAC Key Derivation Function, and HASH is, well, a hash function.
- Prover and server agree on a generator $g$ and a modulus $p$.
- Prover chooses a secret random value $a$ and sends $A = g^a\; \texttt{mod}\; p$ to the server.
- Server chooses a secret random value $b$ and sends $B = g^b\; \texttt{mod}\; p$ to the server.
- Prover locally computes $S = B^a = {g^b}^a = g^{ab}\; \texttt{mod}\; p$.
- Server locally computes $S = A^b = {g^a}^b = g^{ab}\; \texttt{mod}\; p$.
- $K_1 = \texttt{HKDF}(S, 1)$
- $H_1 = \texttt{HASH}(A \| B)$
- $SF = \texttt{HMAC}(K_1, H_1)$
- $H_2 = \texttt{HASH}(H_1 \| SF)$
- $K = \texttt{HKDF}(S, H_2)$
Among the intermediate values, the server only sends $SF$ to the prover. The prover verifies that the received value of $SF$ matches with the locally computed value.
The verifier observes and records $A$, $B$, and $SF$ and also knows $g$ and $p$. He cannot compute $K$ since he does not know the secrets $a$ and $b$. A straightforward way to verify the correctness of $[K]$ is the prover committing to the secret $a$ as the private input in ZKP. Then, using the values known to both prover and verifier, they can compute $[K]$ through the ZKP protocol. This approach, while secure, would be expensive since the circuit for public key operations (modular exponentiations to compute $A$ and $S$) includes a large number of AND gates.
[GZBW22] optimizes this circuit by using the collision-resistance property of hash functions. In the optimized version, instead of committing to $a$, the prover commits to $S$ and the ZKP circuit incorporates steps 6 to 10. Since the verifier already records $SF$ as proxy, the prover opens $[SF]$ after step 8 and the verifier matches it with the recorded value. The collision resistance property of hash functions ensures that the prover cannot come up with a fraudulent value of $S \neq g^{ab}\; \texttt{mod}\; p$ that will result in the same value of $SF$. With this optimization, we avoid executing public-key operations inside the ZKP protocol and are only left with HMAC and HKDF. The most compute-intensive parts of HMAC and HKDF are multiple hash function evaluations (e.g., SHA-256). The hash function’s circuit is quite large, but can be evaluated in reasonable time thanks to recent progress in interactive ZKP.
Note that a TLS session involves multiple keys, and the number of keys depends on the TLS version. TLS 1.3 has four keys: two in each direction for handshake and appdata. $K$ in step 10 above is the appdata key in the direction of the server to the prover. Steps 6 to 10 are repeated in the other direction. In the following section and the next few posts, we focus on server to prover appdata which is the TLS response. At the end of this series, we discuss the prover to server appdata which is the TLS request. DECO also validates the handshake keys in both directions.
Decryption of the TLS Transcript
After key agreement, prover and verifier hold commitment $[K]$ to the TLS session key $K$ and the encrypted TLS response $C$ sent by the server. Prover receives $C$ as the TLS client and verifier records it while acting as the proxy. $C$ is used as the truth known to both the prover and the verifier in the proof of authenticity.
The prover and the verifier first compute a commitment $[R]$ to the TLS response $R$. For this, they need to execute the decryption circuit $R = decrypt(K, C)$ through the ZKP protocol with $[K]$ and $C$ as inputs. TLS supports a number of different cipher suites and the details of $decrypt()$ varies based on the cipher suite chosen for the session. At a high level, $decrypt()$ involves repeated calls to a symmetric cipher (e.g., AES-GCM-128) based on the length of the response. In one of the proof-of-concept applications of DECO with Teller, to decrypt the response (financial report of the prover in this case), around 1700 invocation of AES-128 are required. The AES-128 circuit to decrypt one block (128 bits) consists of 6400 AND gates, which means computing $[R]$ requires computing commitments to more than 10 million AND gate outputs. The memory required to store this many commitments would be prohibitively large. Fortunately, thanks to the ability to forget in commit-and-prove ZKP, we only need enough memory to hold the commitments of a single AES-128 circuit: less than 1GB. More importantly, the memory requirement is independent of the number of invocations of the AES-128 circuit and is thus independent of the size of the TLS response.
At this stage, prover and verifier hold a commitment $[R]$ to the TLS response. Verifier is convinced that the response is authentic since it is decrypted from the encrypted TLS response $C$ that he recorded as a proxy with the committed key $[K]$ that he verified to be computed properly. In the next post, we will describe parsing the already-authenticated response.
This is the second post in a series of DECO research blogs from the Chainlink Labs Research Team. Check out the other posts in the series:
- DECO Research Series #1: An Introduction
- DECO Research Series #3: Parsing the Response
- DECO Research Series #4: Hiding Secret Lengths
References
[GZBW22] Paul Grubbs, Arasu Arun, Ye Zhang, Joseph Bonneau, and Michael Walfish. “Zero-Knowledge Middleboxes”. In USENIX Security Symposium 2022.
