Commit-and-Prove ZKs
This is the third post in a series of ZK-related research blogs from the Chainlink Labs Research Team. Check out the rest of the posts in the series:
Author: Xiao Wang
Contributors: Alex Coventry, Siam Hussain, Dahlia Malkhi, Alexandru Topliceanu, Chenkai Weng, Fan Zhang
In the previous blog, we introduced various metrics to measure circuit complexity and explored how they could be related to the space complexity of a zero-knowledge-proof protocol. The key is to be able to recycle memory as the ZK protocol proceeds.
This post introduces a generic way to do this, known as commit-and-prove zero-knowledge proofs and referred to as a “CnP” scheme. ZK built with CnP provides flexibility in which values to forget and which to keep while proving the circuit. The post focuses on the concepts and basic constructions. An upcoming post will show more efficient constructions of CnP-ZK.
The CnP-ZK Paradigm
The first ingredient of CnP is a commitment scheme. Let’s take a moment to remind what commitments are, because they are such a common and important primitive in cryptography.
Commitment is a common cryptographic protocol that allows one party to put their message in a virtual lockbox so that the receiver won’t be able to see the message until the box is opened by the sender, and the sender won’t be able to change the value once committed.
The second ingredient is the idea of using commitments to “recycle” memory. Given a commitment scheme and a computation circuit, for each gate the prover can always commit to wire values, prove that all commitments can be correctly opened, and prove that the opened values satisfy certain relationships.
It’s worth noting that every ZK protocol can also be made a CnP ZK, though this comes with an extra cost. In particular, this generic approach is done per gate, hence it can be computationally expensive.
Still, now we can use CnP to “recycle” memory: Once a wire is no longer needed in the computation, parties can delete the commitments of that wire from memory. This is why CnP schemes can recycle memory, as we noted at the beginning. Below, we will use our examples from the previous blog to concretely illustrate how this works.
Last, we also present a more advanced CnP ZK that does not require proving the opening of a commitment in circuit. Even this advanced method is presented only for educational purposes, since it has a significant computational cost. As mentioned above, we will not use it once we introduce interaction between parties (this is explored in the next post).
Commitment
To introduce commit-and-prove ZK, we will first talk about commitment. A commitment scheme can be viewed as a locked box: We put a message in the box, lock it, and hand it to another party so that they cannot see it but know that no one can change it. The message can later be opened by sending the key to the receiver. A commitment should be hiding, meaning that the receiver of the box cannot see the message before getting the key; it should also be binding, meaning that once the receiver gets the box, the sender can no longer change the message. Intuitively, commitment gives the receiver the guarantee that the message is decided at the time of sending the commitment.
There are multiple ways to formulate the exact meaning of hiding and binding. For the purpose of this blog, we will take the definition from Introduction to Modern Cryptography (Katz and Lindell) for a non-interactive commitment.
- d := Com(m, r): to commit a message, we pick some randomness r and compute a value d, which will be sent to the receiver.
- Yes/No := Verify(m, r, d): at the time of opening, the sender can send m and r to the receiver, who can verify the validity of the commitment.
In this definition, hiding means that d should not reveal any information about m, and binding means that no sender can find different m and m’ (and r and r’) such that Verify(m, r, d) = Verify(m’, r’, d) = Yes.
In addition to the above two properties, another implicit property of a commitment is that if a commitment is no longer needed, e.g. because it is opened or because computation related to this value has been verified, parties can deallocate the space used to store the commitment values (i.e., d for the receiver and r for the sender). This will be important to improve the space complexity of a zero-knowledge proof (ZKP) scheme.
Commit-and-Prove ZK for Lower Space Complexity
A commit-and-prove ZK scheme is a zero-knowledge proof equipped with commitments. In an ordinary ZK protocol, the prover inputs private witness w, both parties input the function f and the public input x, and the protocol will reveal f(x, w) to the verifier. In contrast, in a commit-and-prove ZK, the prover needs to commit to its private witness before being used in the protocol. Although it looks like extra steps compared to ordinary proofs, it allows us to decide which wires to “remember” and which to “forget” in the execution of a ZK protocol. Throughout the protocol, we prove the computation in a circuit one gate at a time. The protocol maintains the invariant that when we prove the computation of a gate, their input wires are already committed and proven to be correct. To advance to the next gate, the prover should commit to the output wire of the gate and run a small ZKP protocol to prove that the committed output value is correct with reference to the committed input values. Once a committed wire value is no longer needed, because no future gate will use this wire as input, we can forget about the value and its associated commitment. The ability to forget committed wires allows us to prove a circuit computation while recycling the space for wires that are no longer needed. A commit-and-prove ZK protocol supports it as long as the underlying commitment allows “deallocation.”
Let’s revisit the example from the first blog:
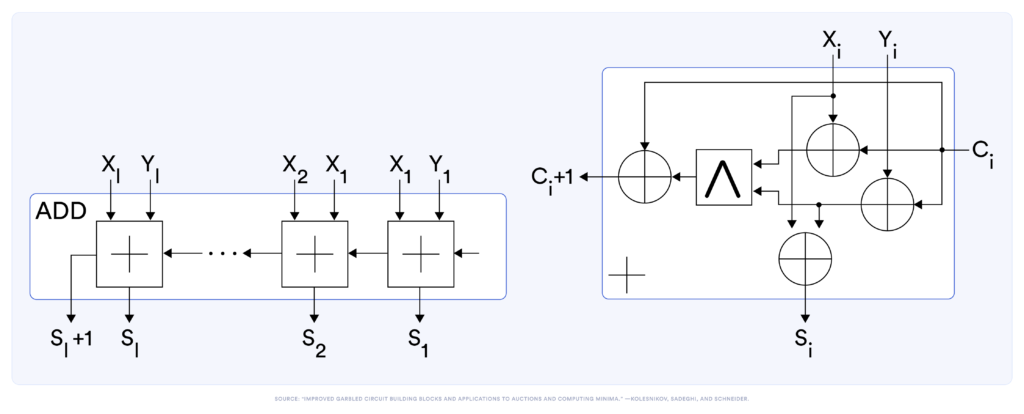
Below, we show a table to prove every gate in the circuit without holding all commitments. In particular, we show in the right column all active, committed wires that one needs to remember.
| % s{1…3} <- 2-bit–adder (x1, x2, y1, y2, c1 ): | Commitments | |
| 1st adder | ||
| (x1, x2, y1, y2, c1) | ||
| Prove t1 = XOR(x1, c1) | (x1, x2, y1, y2, c1, t1) | |
| Prove t2 = XOR(y1, c1) | (x1, x2, y1, y2, c1, t1, t2) | |
| Forget commitment y1 | (x1, x2, y2, c1, t1, t2) | |
| Prove t3 = AND(t1, t2) | (x1, x2, y2, c1, t1, t2, t3) | |
| Forget commitment t1 | (x1, x2, y2, c1, t2, t3) | |
| Prove c2 = XOR(t3, c1) | (x1, x2, y2, c1, t2, t3, c2) | |
| Forget commitments t3, c1 | (x1, x2, y2, t2, c2) | |
| Prove s1 = XOR(x1, t2) | (x1, x2, y2, t2, c2, s1) | |
| Forget commitments x1, t2 | (x2, y2, c2, s1) | |
| 2nd adder | ||
| Prove t4 = XOR(x2, c2) | (x2, y2, c2, s1, t4) | |
| Prove t5 = XOR(y2, c2) | (x2, y2, c2, s1, t4, t5) | |
| Forget commitment y2 | (x2, c2, s1, t4, t5) | |
| Prove t6 = AND(t4, t5) | (x2, c2, s1, t4, t5, t6) | |
| Forget commitments t4, t5 | (x2, c2, s1, t6) | |
| Prove s3 = XOR(t6, c2) | (x2, c2, s1, t6, s3) | |
| Forget commitments t6, c2 | (x2, s1, s3) | |
| Prove s2 = XOR(x2, t3) | (x2, s1, s3, s2) | |
| Forget commitment x2 | (x2, s1, s3, s2) | |
CnP ZK From Any ZK
As briefly discussed in the previous blog, ZKP protocols that process the whole circuit at once often require space linear in the number of gates in the circuit. This becomes a performance bottleneck even when the circuit has a small runtime space complexity. It can be alleviated by converting these protocols to commit-and-prove ZK. Suppose we have a commitment scheme defined as above and any vanilla ZKP scheme (with no special commit-and-prove support natively). As a first step, we will define a statement demonstrating it is possible to prove with any ZK the soundness of commit/prove. As a second step, we will demonstrate how to improve its efficiency.
Suppose H is a cryptographic hash function, then we can define a simple commitment scheme as H(m; r), where H is a random oracle. To ensure hiding, randomness is necessary and must be sufficiently long and sampled freshly for each commitment. Following up on the above example, after committing the input to the input gates, we are in the following configuration. Here the prover has, for each value v, some randomness Rv and its commitment Hv=H(v; Rv).
The prover has values (x1, x2, y1, y2, c1) and (Rx1, Rx2, Ry1, Ry2, Rc1)
The verifier has (Hx1, Hx2, Hy1, Hy2, Hc1), such that Ht = H(t; Rt) for all t.
To prove the first XOR computation, the prover can use any ZK protocol to prove the following statement with (r1, r2, r3, x1, y1, t1) as witness:
“I have values r1, r2, r3, x1, y1, t1, such that Verify(x1, r1)=Yes AND Verify(y1, r2)=Yes AND Verify(t1, r3)=Yes AND (x1 XOR y1==t1).”
This statement has a constant circuit size, so it only needs constant space to prove with any ZK protocol. Once the verifier is convinced, the ZK proof does not need to be stored.
Note that while the above example shows that commit-and-prove is feasible, it’s very inefficient (proving one gate involves proving three commitment verification). In the next section, we will take a detour and show a more efficient solution without the need to prove verification as part of the statement. Readers who are interested in the interactive ZK can directly jump to the next blog, while readers who are curious about the details of this protocol are encouraged to proceed. The protocol is by Groth, Ostrovsky, and Sahai (EUROCRYPT 2006), and understanding the protocol requires some background in cryptography and a basic understanding of group theory and bilinear maps.
A Better CnP ZK
The GOS construction also starts from a commitment scheme where the messages to be committed are prime-order field elements (think of integers modulo a prime). The commitment scheme is more powerful; in addition to Commit and Open procedures, it also supports two more features:
- The scheme is additive homomorphic. This means that if the prover commits to m1 and m2 in two separate commitments, then the verifier can compute a valid commitment to m1+m2 without the help of the prover.
- The scheme allows checking if the underlying committed message is binary or its value is greater than 1.
In the GOS paper, the authors showed how to construct such a commitment scheme based on bilinear maps. One crucial observation is that for a NAND gate, any x, y ∈ {0, 1} and any integer z:
z = x NAND y if and only if x + y + 2z -2 ∈ {0, 1}
This can be verified from the following table:
| x | y | z=X NAND y | x+y+2z-2 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
We focus on NAND gates because they are functionally complete, meaning that any computation can be represented as a sequence of NAND gates.
Inspired by this relationship, checking a NAND gate can be reduced to checking that a wire value is binary, which can be converted into problems simpler to check. In more detail, with the prover committed to x, y and z, two parties just need to perform the following two steps to verify that z = x NAND y:
- Homomorphically compute a commitment to b = x+y+2z-2.
- Check that b is a binary value.
To check that a committed value is indeed binary, the GOS paper provided 2 different protocols both only requiring a constant number of public-key style operations. Interested readers can find more details in their paper.
This CnP-ZK protocol is non-interactive with costs less than proving a commitment scheme in ZK. It can be reasonable for small statements but still orders of magnitude slower than cleartext computation. In the next post, we will introduce interactive CnP-ZK protocols, which require some rounds of communication between the prover and the verifier but achieve very high computational efficiency.
Further Reading
The CnP-ZKP paradigm was first discussed by Kilian (89, in his dissertation) and formalized by Canetti, Lindell, Ostrovsky, and Sahai (STOC 02’). There have been many practical ZK protocols supporting this feature, including zero-knowledge based on garbled circuits (Jawurek et al. CCS 13’), LegoSnark (Campanelli et al. CCS 19’), VOLE-based ZK (Weng et al. S&P 20) and many others.
