Author: Siam Hussain

Contributors: Lorenz Breidenbach, Dahlia Malkhi, Alexandru Topliceanu, Xiao Wang, Chenkai Weng, Fan Zhang

DECO enables a user to prove the authenticity of data and claims about it without revealing the data itself. Authenticity, in this context, means that the data is obtained from a specific web server through the TLS protocol. For example, a user can prove that she obtained her financial report from her bank’s website and that, according to this report, her account balance is above a particular amount. However, she does not reveal any other information present in the report, such as her account number or exact balance. 

DECO requires no server side cooperation. The TLS server does not have to be modified or even be aware that it is participating in the DECO protocol, greatly simplifying DECO’s path to adoption. 

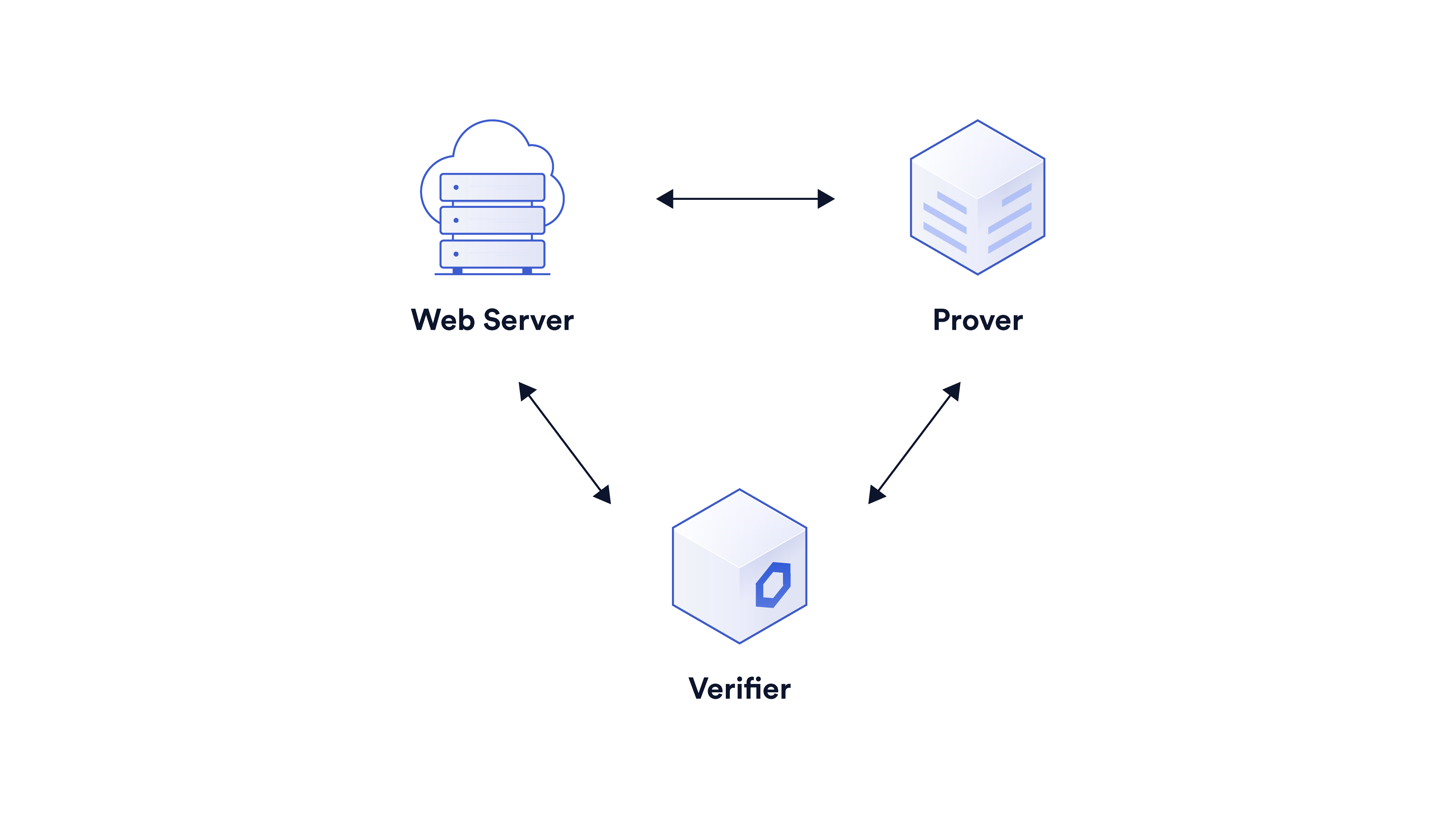
With this post, we begin a mini-series of articles describing the challenges in the progress of DECO from an academic publication [ZMMG+20] to a product, how it makes use of an interactive zero-knowledge core, and some of the optimizations aiding its real-life deployment. If you are interested in the motivation behind DECO and its various use cases, this talk is a good place to start. In this introductory post, we provide a brief overview of DECO and one of its key ingredients: zero-knowledge proofs (ZKPs). 

A (Very) Brief Overview of Interactive Zero-Knowledge Proofs (ZKPs)

DECO harnesses the magic of ZKPs to ensure privacy. In TLS, the identity of the server is verified using fresh challenges generated by the client for every session. This makes TLS, and in turn DECO, interactive protocols. Therefore, we use an interactive “commit-and-prove” form of ZKP called VOLE-based ZKP in order to benefit from its higher speed, lower memory footprint, and scalability compared to non-interactive ZKP. We provide a brief overview of the protocol here. Please see our blog series on interactive ZKPs for details. 

Commitments are a cryptographic concept that can be viewed as a locked box. The prover committing to a variable $x$ is analogous to putting $x$ in a locked box and sending it to the verifier. The verifier cannot view the committed value but has the guarantee that the prover cannot change it once sent. Later, the prover can send the key to the verifier to open the commitment. We denote the commitment to $x$ with $[x]$. 

Given commitments to the inputs of a logic gate (AND/XOR), a commit-and-prove ZKP protocol enables the prover and verifier to compute the commitment to the output. This in turn enables the prover to prove the correct computation of a circuit consisting of these gates through the following steps: 

(i) The prover commits to the inputs of the circuit.

(ii) Together the prover and the verifier compute the commitments to the outputs of the gates going through them in topological order.

(iii) The prover opens the commitments to the outputs of the circuit. 

The commitment scheme used in the DECO ZKP core is additively homomorphic. This means that the commitment to the output of an XOR gate (addition modulo 2) can be computed locally without incurring any communication or computation cost. The cost of evaluating a circuit through the ZKP protocol is thus linear in the number of AND gates. 

Upcoming Posts

Over the next few weeks we will publish a series of blogs under the tag DECO Series discussing the details of different steps of the DECO protocol. Here is a sneak peek into the upcoming posts: 

• Proving the authenticity of data: In the first step of the DECO protocol, the prover convinces the verifier that a TLS response is obtained from a particular server. This procedure closely follows the steps in the TLS protocol. First, prover and server generate a set of symmetric keys to encrypt the TLS request and response. Then the prover decrypts the ciphertext received from the server to obtain the response. The verifier does not see either the key or the response. However, he actively participates in the protocol to ensure that the prover correctly computes the key, the response, and the ZKP commitments to them. In this post, we describe how the verifier participates in the TLS protocol and verifies the authenticity of the response. 
• Parsing the response: After the verifier is convinced of the authenticity of the response, the next step is to parse the response efficiently and reliably to retrieve relevant information. The primary challenge in this step is verifying the correctness of parsing without accessing sensitive information in the response. 
• Hiding the length of the sensitive data: The ZKP protocol employed in DECO, and a majority of ZKP protocols in general, hide the values of the private data but not their different lengths. In this post, we describe how DECO enables hiding the lengths of individual secrets within the TLS interaction.
• Proofs over multiple responses: For some use cases of DECO, the claims involve information retrieved from multiple responses, possibly over multiple TLS sessions (and from multiple sources). In this post, we describe how DECO combines such responses into one coherent proof.
  

This is the first post in a series of DECO research blogs from the Chainlink Labs Research Team. Check out the other posts in this series: 

• DECO Research Series #2: Provenance and Authenticity
• DECO Research Series #3: Parsing the Response
• DECO Research Series #4: Hiding Secret Lengths

References

[ZMMG+20] Fan Zhang, Deepak Maram, Harjasleen Malvai, Steven Goldfeder, and Ari Juels. “DECO: Liberating Web Data Using Decentralized Oracles for TLS.” In ACM Computer and Communications Security 2020.