Realizing VOLE
This is the sixth post in a series of ZK-related research blogs from the Chainlink Labs Research Team. Check out the rest of the posts in the series:
- Introduction to Interactive Zero-Knowledge Proofs
- Background on Computation Complexity Metrics
- Commit-and-Prove ZKs
- VOLE-Based ZK
- VOLE-Based Interactive Commitments
Author: Chenkai Weng
Contributors: Siam Hussain, Dahlia Malkhi, Alexandru Topliceanu, Xiao Wang, Fan Zhang
Synopsis
In the previous post, we introduced VOLE-based interactive commitment assuming there is a way to construct VOLE correlations efficiently. In this post, we describe an efficient protocol to generate VOLE correlations for batches of commitments.
In the previous blog we saw that in VOLE setup phase, prover receives $\mathbf{m}$, $\mathbf{r}$ and verifier receives $\mathbf{k}$, $\Delta$, where $\mathbf{m}$, $\mathbf{r}$, $\mathbf{k}$ are length-$N$ vectors. In VOLE setup based on the conventional oblivious transfer extension protocols ([IKNP03], [ALSZ15]), for any arbitrary committed value $\mathbf{r}$ requires communication overhead linear to $N$. Recent works based on the Learning Parity Noise (LPN) assumption allow generating $N$ random VOLE correlations with communication cost sublinear to $N$. It needs the following two ingredients:
$(i)$ $h$ random VOLE correlations where $h \ll N$.
$(ii)$ $N$ VOLE correlations with sparse committed values.
The VOLE correlations in the first ingredient can be generated by traditional VOLE protocols with cost linear to $h$, since $h \ll N$. In this post, we first explain how to generate the second ingredient, which is a special VOLE functionality where imposing the condition of the committed value to be sparse (Hamming weight $\ll N$) allows us to reduce the cost to be sublinear in $N$. Then we discuss how LPN combines them into $N$ VOLE correlations with no further communication needed.
The VOLE Construction
The VOLE correlations can be efficiently generated based on the learning parity with noise (“LPN”) assumption [BCGI18]. Apart from LPN, an important building block is the single-point VOLE (SPVOLE), where the prover commits to a vector of bits that are all zeros except at one location. We begin by describing SPVOLE and then explain how to use them. Note that VOLE is a two-party protocol. To make it consistent with the previous posts in the ZK scenario, we continue to denote two parties as the prover and the verifier.
Single-Point Vector Oblivious Linear Evaluation (SPVOLE)
The single-point length-$n$ VOLE is a special VOLE functionality. It provides a prover with:
- A length-$n$ vector $\vec{f}$ of which all elements belong to $\mathbb{F}_{2^{128}}$.
- A length-$n$ vector $\vec{e}$ of which all elements belong to $\mathbb{F}_2$. The Hamming weight of $\vec{e}$ is only 1. This means that there is only one entry which is 1 while all other entries are 0. The index of this entry is kept secret from the verifier.
Correspondingly, the verifier obtains:
- A global key $\Delta$ that belongs to $\mathbb{F}_{2^{128}}$.
- A length-$n$ vector $\vec{s}$ of which all elements belong to $\mathbb{F}_{2^{128}}$.
These vectors satisfy $\vec{f}=\vec{s}-\Delta\cdot\vec{e}$.
Observe that the vectors $\vec{f}$ and $\vec{s}$ contain the same elements at $n-1$ entries, but differ by $\Delta$ at only one entry. The communication complexity for executing SPVOLE protocol is $\mathcal{O}(\log n)$. A construction of SPVOLE will be explained in the next post.
Multi-Point Vector Oblivious Linear Evaluation (MPVOLE)
The VOLE protocol generating $N$ correlations employs an MPVOLE sub-protocol that generates the second ingredient: $N$ VOLE correlations with sparse committed values.
MPVOLE works with additional parameters $n, t$, such that $n = N / t$. It involves invoking SPVOLE $t$ times and concatenating the generated vectors. Each invocation $i$ of SPVOLE generates SPVOLE correlations $\vec{f}_i = \vec{s}_i-\vec{e}_i\cdot\Delta$ where dimension of the vectors $\vec{f}_i$, $\vec{s}_i$, and $\vec{e}_i$ is $n$. The global key $\Delta$ is identical for all invocations. Define $\|$ as a symbol for concatenation. Eventually the prover holds $\vec{f} = (\vec{f}_1 \| \ldots \| \vec{f}_t)$ and $\vec{e} = (\vec{e}_1 \| \ldots \| \vec{e}_t)$ and the verifier holds $\Delta$ and $\vec{s} = (\vec{s}_1 \| \ldots \| \vec{s}_t)$. The concatenated vector $\vec{e}$ has dimension $N$ and Hamming weight $t \ll N$. Note that the communication cost for MPVOLE is $\mathcal{O}(t \log N/t)$.
Learning Parity With Noise (LPN)
LPN is one of the cryptographic hardness assumptions that contribute to various encryption, authentication, and advanced cryptographic protocols.
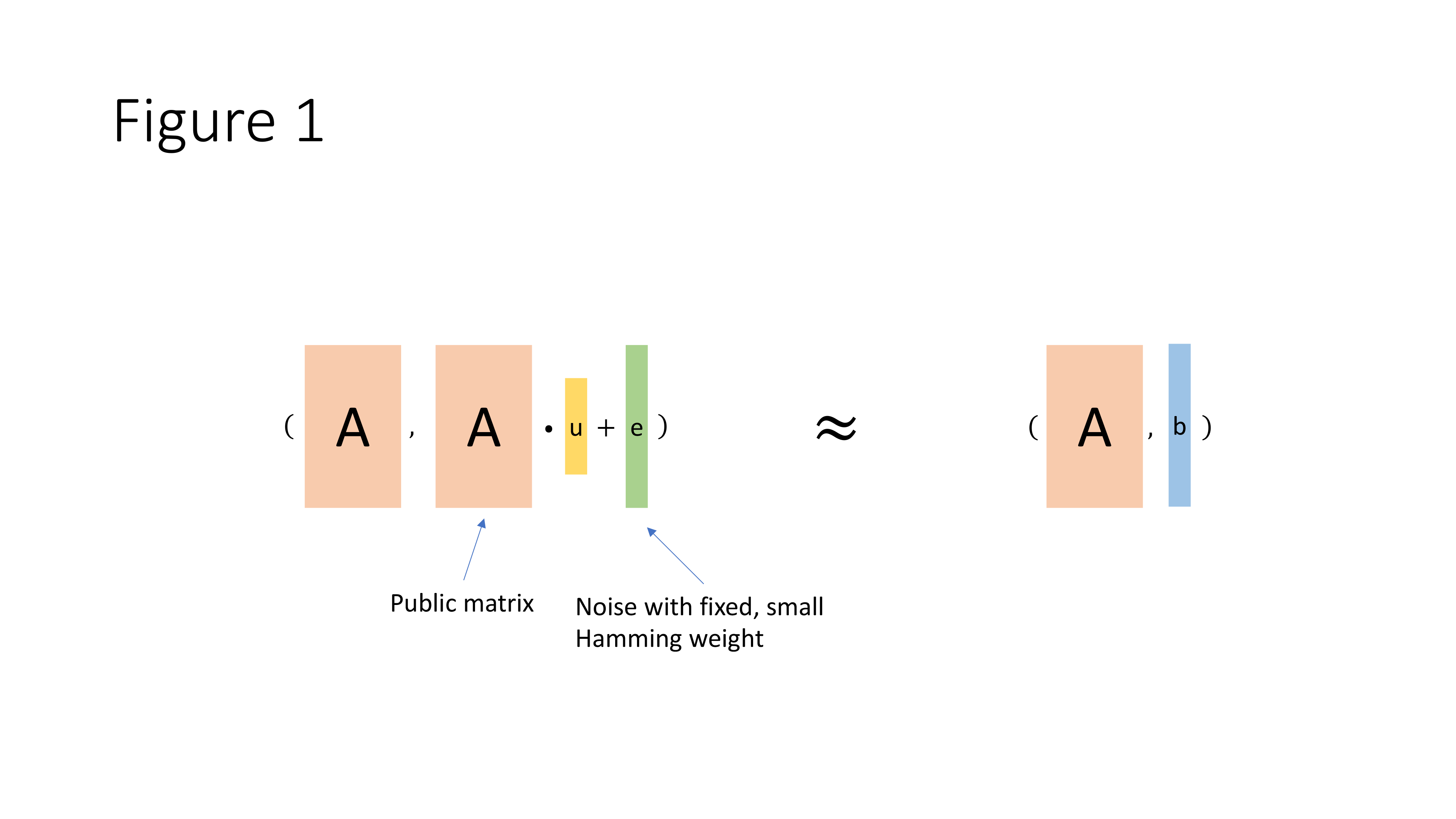
As shown in the picture below, define parameters $(N, h, t)$ such that $N \gg h \gg t$. We start by sampling the following elements that will be used to compute values to be sent to the adversary:
- Randomly sample a matrix $A$ of dimension $N \times h$.
- A random vector $\vec{u}$ of dimension $h$.
- Randomly sample a sparse vector $\vec{e}$ of dimension $N$ and Hamming weight $t$.
The LPN assumption states that for any polynomial-time adversary with $A$ but not $\vec{u}$ and $\vec{e}$, it cannot distinguish between $\vec{u}A + \vec{e}$ and a uniformly random Boolean vector $\vec{b}$. In other words, $\vec{u}\cdot A + \vec{e}$ looks pseudorandom to the adversary.
Putting Everything Together
We now combine MPVOLE and LPN to realize the VOLE functionality. At a high level, we use the LPN assumption to expand a small number of VOLE correlations to a large number of VOLE correlations. As demonstrated in the figure below, this consists of 3 steps.
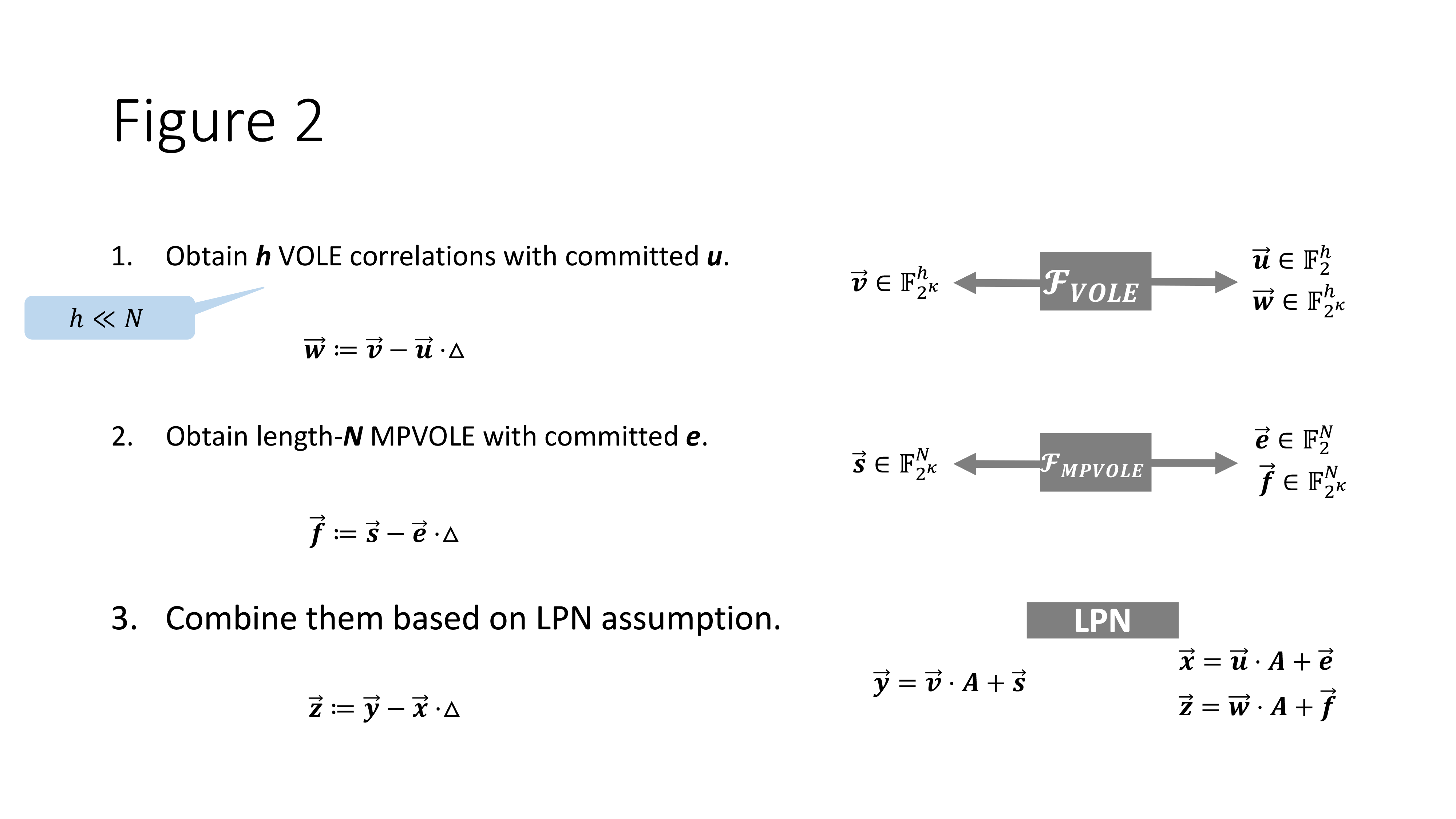
Two parties first generate $h$ VOLE correlations of uniformly random committed value $\vec{u}$. This is done through the oblivious transfer extension protocols with linear communication cost. However, since $h \ll N$ the cost is far smaller than generating $N$ correlations directly. Then they invoke MPVOLE to generate commitment for the sparse noise vector $\vec{e}$ in LPN. This step incurs a communication cost of only $\mathcal{O}(t \log N/t)$. Finally, they apply the LPN assumption to expand the random length-$h$ VOLE correlation of $\vec{u}$ to random length-$N$ VOLE correlation of $x$ . This step only involves local computation.
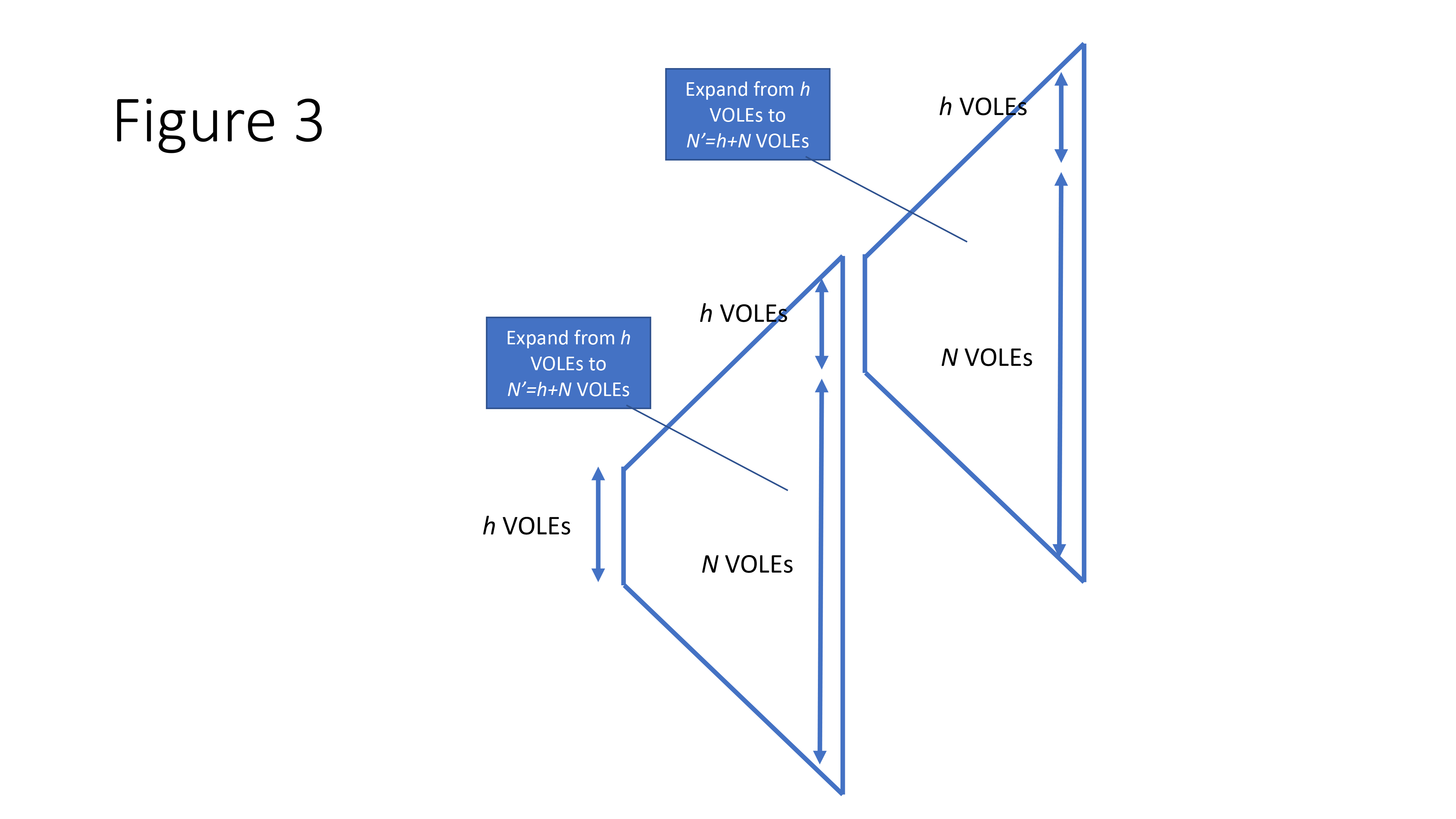
Bootstrapping. With the communication cost of VOLE setup sub-linear in $N$, the main constraint on the value of $N$ is posed by the available memory in the system. The bootstrapping process enables repeated execution of the above VOLE protocol without repeating the oblivious transfer extension to generate VOLE correlation of $\vec{u}$, thus further reducing the amortized cost. Remember that a small number of VOLE correlations are needed at steps 2. Define $N’ = N + h$ and the parties generate $N’$ VOLE correlations during each expansion. Then $h$ of them will be preserved for the next epoch of expansion for the generation of $\vec{u}$ and $\vec{e}$. In this way, no oblivious transfer extension is needed after the first expansion.
The History of VOLE
The LPN-based VOLE is first proposed in [BCGI18], where two parties locally expand a pair of short correlated seeds into a large number of pseudorandom VOLE correlations. Its security relies on LPN assumption over large fields. Here a large field implies a field $\mathbb{F}_p$ where $p$ is an exponentially large prime number, unlike the $\mathbb{F}_2$ used in the protocol described in our blog series. A follow-up work [BCGI19] proposes a VOLE construction that operates over field $\mathbb{F}_2$ and achieves lower communication complexity compared to all previous works on VOLE. Together they serve as the foundation for LPN-based VOLE protocols. [SGRR19] and [YWLSW20] further improves the performance of VOLE over $\mathbb{F}_p$ and $\mathbb{F}_2$, respectively.
[IKNP03]
Ishai, Yuval, Joe Kilian, Kobbi Nissim, and Erez Petrank. “Extending Oblivious Transfers Efficiently.” In Crypto, vol. 2729, pp. 145-161. 2003.
[ALSZ15]
Asharov, Gilad, Yehuda Lindell, Thomas Schneider, and Michael Zohner. “More efficient oblivious transfer extensions with security for malicious adversaries.” In Advances in Cryptology–EUROCRYPT 2015: 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, April 26-30, 2015, Proceedings, Part I, pp. 673-701. Berlin, Heidelberg: Springer Berlin Heidelberg, 2015.
[BCGI18]
Boyle, Elette, Geoffroy Couteau, Niv Gilboa, and Yuval Ishai. “Compressing vector OLE.” In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, pp. 896-912. 2018.
[BCGI19]
Boyle, Elette, Geoffroy Couteau, Niv Gilboa, Yuval Ishai, Lisa Kohl, and Peter Scholl. “Efficient pseudorandom correlation generators: Silent OT extension and more.” In Advances in Cryptology–CRYPTO 2019: 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 18–22, 2019, Proceedings, Part III 39, pp. 489-518. Springer International Publishing, 2019.
[SGRR19]
Schoppmann, Phillipp, Adrià Gascón, Leonie Reichert, and Mariana Raykova. “Distributed vector-OLE: improved constructions and implementation.” In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, pp. 1055-1072. 2019.
[YWLZW20]
Yang, Kang, Chenkai Weng, Xiao Lan, Jiang Zhang, and Xiao Wang. “Ferret: Fast extension for correlated OT with small communication.” In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security, pp. 1607-1626. 2020.
