Optimal Latency and Communication SMR View-Synchronization
Authors: Andrew Lewis-Pye (London School of Economics), Dahlia Malkhi (Chainlink Labs), Oded Naor (Technion and Starkware)
A previous post described the Byzantine View Synchronization (“BVS”) problem and why it turned into a bottleneck of leader-based consensus protocols for the partial synchrony setting. That post tackled single-shot consensus, and presented an evolution of BVS solutions (“Pacemakers”) that finally brought BVS communication down to $O(n^2)$ messages—the optimal, according to a known lower bound—in the worst case.
In this post, we expand the discussion to multi-shot consensus protocols, also known as State-Machine-Replication (SMR).
Briefly, in the BVS problem, a group of processes enter/leave views until they reach a view (“Synchronized View”) with an honest leader and spend sufficient time in overlap in the view for the leader to drive a consensus decision. The multi-shot setting, that is, SMR, requires solving BVS infinitely many times.
Existing BVS protocols (some of which were described in the previous post), exhibit an undesirable tradeoff in the multi-shot setting: Each time a Byzantine leader is encountered following a succession of honest leaders, protocols either incur a high communication overhead (quadratic), or a high expected latency (linear).
This post surfaces this problem and presents a new protocol, Lumiere, that quickly recovers (namely, within a constant latency) in case of a Byzantine leader, while retaining optimal communication and latency both in expectation and in the worst case.
Preliminaries
The system consists of $n$ nodes, $n\geq 3f+1$, where $f$ is a bound on the number of Byzantine nodes.
A view $v$ is considered Coordinated when all honest nodes are in the same view for a sufficiently long time $\Gamma$ (dictated by the underlying SMR protocol). This is usually achieved when the honest nodes enter view $v$ within some known time bound—typically two network delays—from one another.
A Coordinated View is Synchronized if it has an honest leader. A Pacemaker is a protocol used by the underlying SMR protocol to reach an infinite number of Synchronized Views.
Some Pacemakers (e.g., the Pacemaker solution by Lewis-Pye) incorporate specific view consensus protocols, but generally, the in-view consensus protocol is opaque while always requiring participation by $2f+1$ nodes. For example, in HotStuff, the view protocol consists of all nodes sending votes to the leader, the leader collecting $2f+1$ votes and forming a quorum-certificate (“QC”) which is a threshold aggregate of votes. It then sends the QC back to the nodes. A QC for view $r$ proves that a decision was reached in the consensus protocol in that view.
It will also be useful to introduce into the discussion two additional parameters: $\Delta$ is a parameter known to the protocol and denoted the estimated network delay after GST. The actual network delay is denoted by $\delta$. It is assumed that, after GST, $\delta \leq \Delta$. $\Gamma$ is the presumed interval needed to reach a decision in single consensus instance within a Synchronized View. We will assume $\Gamma = O(\Delta)$.
The Pacemaker due to Lewis-Pye (2022)
In this section, we describe the Pacemaker protocol by Lewis-Pye (“LP-22”). This Pacemaker achieves optimal worst-case complexity and latency, and is also responsive. That is, if there is a sequence of honest leaders once a Synchronized View is reached, then decisions are made at network speed $\delta$ until the first occurrence of a Byzantine leader.
The high-level pseudocode of LP-22 is the following. Each sequence of $f+1$ consecutive views $e, \dots, e+f$, where $e \bmod (f+1)=0$, is called an epoch. If $r=0 \bmod (f+1)$, then view $r$ is called an “epoch-view”.
- At any point, if a node is in view $r$ and receives a threshold signature Epoch Certificate (EC) for an epoch-view $r’>r$, then it sends that EC to all nodes and enters view $r’$.
- If a node wishes to enter view $r$, where $r \bmod (f+1) = 0$, it performs an “epoch-view” procedure for view $r$:
- Send (WISH,r) to $f+1$ view leaders in the epoch.
- A leader collects $2f+1$ (WISH,r) messages, forms a Epoch Certificate (EC) for view $r$, and sends this to all nodes.
- If a node wishes to enter view $r$, for $r \bmod (f+1) \neq 0$ (a non epoch-view), it enters.
- A node wishes to enter view $r$ if either:
- Its view $r-1$ timer expires.
- The node receives a certified decision (QC) by the leader of view $r-1$.
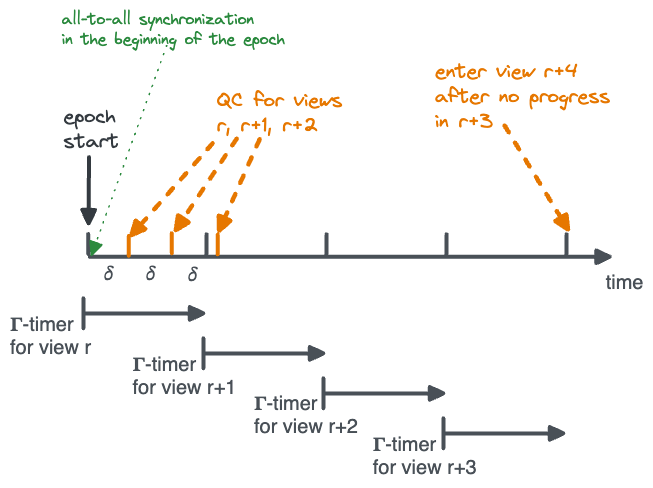
- If a node enters view $r$ such that $r \bmod (f+1) = 0$ at time $s$ (say), it sets a view $r+k$ timer to expire at time $s + (k+1)\cdot \Gamma$, for each $k=0, \dots ,f$.
A related work named RareSync has an identical approach to LP-22 at a high-level, but employs Bracha-style all-to-all broadcast, rather than using $f+1$ leaders as relays. It also doesn’t have responsiveness: LP-22 achieves responsiveness by advancing views inside an epoch when receiving a certified decision. By adding this simple condition, a succession of honest leaders in a single epoch can drive progress and make new decisions at network speed. If the actual network speed is faster than the timeout period, then this Pacemaker dramatically improves the actual latency compared to RareSync in runs with no faulty leaders.
Note, though, that if the $k$-th view of an epoch has a faulty leader, then nodes must wait for the predetermined $(k+1) \cdot \Gamma$ timeout to advance to the next view (see depicted below). This means that even a single Byzantine leader can cause significant delays, especially in views toward the end of the epoch. We will get to this next.
Lumiere
In a previous post, we saw earlier Pacemaker protocols (like Cogsworth, NK-20, FastSync) that actively synchronize views on a need-only basis, each time a bad leader is encountered. Each synchronization event has only $O(\Delta)$ latency, but it might incur quadratic communication cost; hence, the overall worst-case communication cost is $O(n^3)$.
On the other hand, as we saw above, LP-22/RareSync synchronize views upfront, on an epoch basis, which is not latency-optimal. However, their worst-case communication complexity is optimal (quadratic).
This seeming tradeoff leaves open the following natural question:
Does a responsive Pacemaker protocol exist that has optimal worst-case communication complexity (quadratic), and allows nodes to progress after a bad leader within $O(\Delta)$ latency?
Lumiere answers this question affirmatively. It combines methods from both Cogsworth/NK-20 and LP-22/RareSync; and borrows from Fever a core technique (which was applied in a setting with real-time clocks, and with different guarantees) of advancing clocks forward to provide responsiveness.
Overview of Lumiere:
In Lumiere, nodes synchronize at the start of each epoch and set view timers $(k+1) \cdot \Gamma$ for $k= 0, \dots , f$ (same as LP-22).
By default, nodes wish to enter a view (say $r+1$) within an epoch upon expiration of these timers. However, nodes may wish to enter view $r+1$ early upon obtaining a QC in view $r$.
Whenever nodes wish to enter a view $r+1$ within an epoch (potentially early), they re-synchronize entering view $r+1$ via the (linear) procedure below.
To enter view $r+1$, a node performs two actions:
- The node sends a view message to the next leader. When a leader collects $f+1$ view messages, it forms a View Certificate (VC) and sends it to all nodes. Upon receiving a VC for any view higher than its current, a node enters the view.
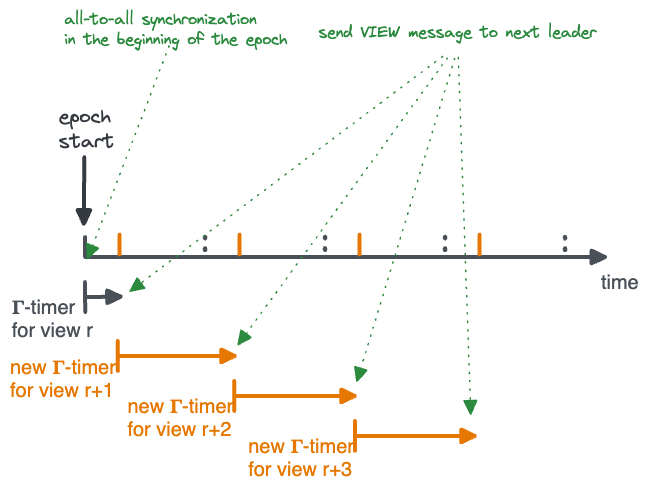
- Whenever a node obtains a VC, the node adjusts its future view timers to start now. For example, say that $\Gamma/2$ elapsed since the node advanced to view $r$ until it obtained a VC for view $r+1$; see depicted below. Then the node sets the timer for view $r+1$ to expire $3\Gamma/2$ after view $r$ was entered, instead of after $2\Gamma$ as originally. (If the node obtains a VC for $r + 2$ earlier, it may again adjust its timers and advance to $r+2$ responsively as well, and so on.)
The figure below depicts the Lumiere protocol. When the epoch begins, there’s an all-to-all synchronization after which each view lasts $\Gamma$. Now suppose a QC is received in the first view (orange line).
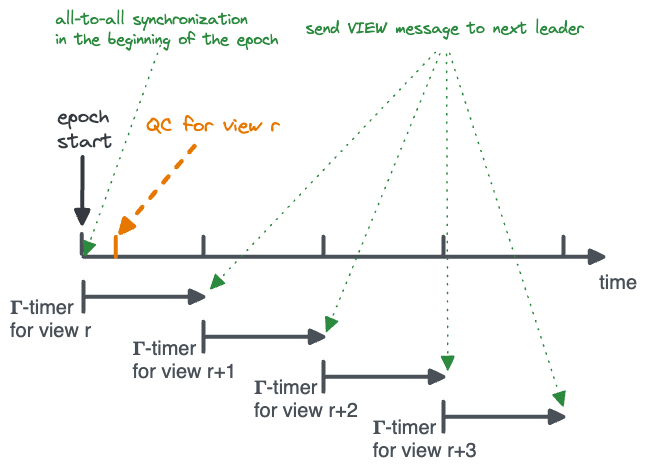
After the QC and the next VC are received, the timeouts of the succeeding views are adjusted (orange lines).
Pseudocode of Lumiere:
A node in view $r-1$ performs the following actions:
- If the node wishes to enter view $r$, where $r \bmod (f+1) = 0$, it performs an “epoch-view” procedure for view $r$, as in LP-22/RareSync. As before, ECs for epoch-views require $2f+1$ WISH messages.
- If a node wishes to enter view r, for $r \bmod (f+1) \neq 0$ (a non-epoch-view):
- send (VIEW,r) to the leader of $r$
- a leader that receives $f+1$ VIEW messages for view $r$ forms a threshold signature View Certificate (VC) and broadcasts it to all nodes
- A node advances to view $r$, where $r$ is higher than the view the node is currently in, if it sees either an EC or a VC for view $r$. In this case, suppose the current time is $s$ and proceed as follows. For each view $r’\geq r$ in the same epoch, set the timer for view $r’$ to expire at time $s+(r’-r+1) \cdot \Gamma$.
- A node wishes to advance to view $r+1$ in the following two cases:
- The timer for view $r$ expires.
- If it obtains a QC for view $r$.
Correctness sketch:
The key insight is that if a view $r$ generates a QC, at least $f + 1$ correct nodes must have entered view $r$ to facilitate progress. Hence, when the first correct node $P$ advances to an early re-synchronization from view $r$ to view $r+1$, there are at least $f$ nodes who will try to enter views $r+1$, $r+2$, …, each within a $\Gamma$ gap behind $P$.
Consider the first two consecutive correct leaders, $r’, r’’$, following $r$. There are two cases:
- If any correct node $P$ expires $r’$ and sends a view message for $r’’$ before the leader of $r’$ sends a VC, $f$ bad nodes can send view messages and enable $P$ to enter $r’’$. However, since the leader of $r’’$ is correct, all nodes enter $r’’$ within $\Delta$ of its leader sending a VC.
- Otherwise, all correct nodes overlap in $r’$ sufficiently long to form a QC in $r’$.
Optimistic Asynchronous Atomic Broadcast
It is worthy of mentioning a different approach for tackling view-change, which was introduced in two recent advances, Ditto-21, BoltDumbo-21. These protocols are not per se partially synchronous; they actually revisit optimistic asynchronous atomic broadcast, an approach which was pioneered in KS-02, RC-05, and generalized in 700bft-10. The idea is to have an optimistic partially synchronous regime achieving optimistically optimal work (linear), and use a quadratic asynchronous protocol as a fallback mechanism during asynchronous periods.
Since there is no view-change in these solutions, and the fallback regime is fully asynchronous, there is no required view-synchronization per se. This works as follows.
When a view fails to make progress for $\Gamma$, instead of replacing the leader and proceeding with the next leader, nodes fall back to a full-fledged asynchronous consensus protocol. Internally, the quadratic asynchronous regime borrows from VABA. More specifically, it invokes $n$ simultaneous HotStuff consensus instances, one per node acting as candidate leader. After $n-f$ instances complete, it elects in retrospect one node as leader unpredictably and uniformly at random. If the leader is honest, the protocol will have reached a decision by this leader; otherwise, the protocol invokes another wave of $n$ HotStuff instances, each of which orchestrates a view-change from the elected leader.
Running $n$ simultaneous views, electing a random leader, and orchestrating $n$ view-changes from it to the next instance, incur only a total quadratic cost (relying on the HotStuff linear in-view/view-change regimes). Note, however, that each time a Byzantine leader is elected within the asynchronous consensus protocol the complexity is quadratic, and a fortiori, an unlucky series of $f$ leader failures leads to a worst-case $O(n^3)$ complexity.
Performance of Various Pacemakers
The table below compares the latency and message complexity achieved by state-of-the-art protocols for reaching $n$ consensus decisions after the first synchronization. We consider $n$ consensus decisions, rather than single-shot, because the single-shot figures can often hide what happens in the aggregate. For example, Lumiere has optimal (worst-case) $O(n^2)$ message complexity for reaching a single consensus decision, but also has $O(n^2)$ complexity for reaching $n$ decisions. We consider what happens after first synchronization because the latency and complexity required for the first synchronization are sometimes special cases–the measures shown below aim at presenting what is important in contexts where one must deal with occasional periods of asynchrony but long periods of synchrony are the norm.
Defining the measures. Intuitively, we are interested in the communication cost and latency incurred in a succession of views reaching $n$ consensus decisions, measured after GST and starting with a synchronized view. In order to provide an apples-to-apples comparison of protocols, we present explicit formulae, parametrized by a random variable $f_m$ denoting the actual number of views with faulty leaders in the succession.
More formally, let $t^{\ast}$ be the first synchronization time after GST, i.e. the first time $t^{\ast}$ after GST such that all honest players are in the same view with honest leader from time $t^{\ast}$ until that view produces a QC. Let $t$ be any time after $t^{\ast}$. Let $v$ be the greatest view any honest player is in at $t$. Define $v’$ to be the least view $>v$ such that $n$ views in the interval $[v,v’]$ produce QCs (by some least time $t’$, say), and define $f_m$ to be the number of views in $[v,v’]$ that have faulty leaders. Latency is $t’-t$. Message complexity is the number of messages sent by honest players during $[t,t’]$. This includes messages sent while carrying out both the View Synchronization protocol and the underlying protocol. Note that $v’$ could potentially be infinite (depending on the protocol), in which case we define $t’=\infty$.
View timer: It is assumed that each protocol has a per-view timer $\Gamma$ to expire a view, satisfying $O(\Gamma) = O(\Delta)$.
Full consensus protocol: When it comes to “pure” View Synchronization methods, e.g., Cogsworth or NK-20, we assume HotStuff is used as the core consensus mechanism.
Insights: Cells marked with a green sparkle (❇️) indicate improvement relative to higher rows; a warning sign (⚠️) indicates trading off some desirable property relative to it. Briefly, the figures shown underscore an evolution as follows:
- The first row considers Cogsworth, which is optimistically communication and latency optimal against benign failures, but each Byzantine leader may inflict $O(n^2)$ communication overhead, hence the worst case is $O(n^3)$.
- The second row considers NK-20, which improves the expected communication cost inflicted by $f_m$ Byzantine leaders to $(f_m \cdot n)$, but a succession of $f_m$ bad leaders can cause $O(n \cdot f_m^2)$ communication overhead, and the worst case remains $O(n^3)$.
- The third and fourth rows consider several protocols that employ a quadratic View Synchronization sub-protocol on a need-only basis each time progress is stalled. They are latency optimal: in fail-free executions, they incur $O(n \cdot \delta)$ latency, and in executions that encounter $f_m$ bad leaders, they incur an extra $O(f_m \cdot \Delta)$ delay (the optimal).
However, the downside is that they incur a quadratic communication cost in synchronization overhead each time a bad leader is encountered, i.e., a total of $O(f_m \cdot n^2)$ synchronization overhead. The worst-case communication remains $O(n^3)$. - The fifth row of the table includes the LP-22 and RareSync protocols, which invest a quadratic communication cost upfront, achieving worst-case communication optimality ($O(n^2)$).
However, waiting for pre-synchronized times has an expected $O(n \cdot \Delta)$ delay when bad leaders are encountered. Hence, except in fail-free executions, they incur a higher expected latency than previous protocols. - The sixth row of the table presents a recent protocol named Fever, which retains the good properties of previous protocols but removes the expected $O(n \cdot \Delta)$ delay of the fifth row. Fever introduces a new requirement, namely that all nodes start the execution at the same time. Because of this assumption, Fever does not rely on epoch synchronizations and does not fall out of sync during periods of asynchrony, a desirable property that is not exhibited in the table below.
- The seventh row of the table presents the performance measures of the Lumiere protocol. Lumiere keeps the expected $O(\Delta)$ latency of Fever without relying on a synchronous start, commencing at the first epoch after communication has stabilized (as defined above), while retaining communication optimality.
| Pacemaker | Latency | Communication | Live Against Asynchrony | Initial Clock Sync |
| Cogsworth-19 | Expected: $(f_m \cdot \Delta + n \cdot \delta)$
Worst case: $O(f_m^2 \cdot \Delta + n \cdot \delta)$ |
Expected (against benign failures): $O(f_m \cdot n + n^2)$
Worst-case (against active Byzantine attack): $O(f_m\cdot n^2 + n^2)$ |
no | Not required |
| Naor-Keidar-20 | same as above | Expected: $O(f_m\cdot n+ n^2)$
❇️ Worst case: $O(n \cdot f_m^2 +n^2)$ |
same | same |
| FastSync-20 / DiemBFT-v4-21 / R-20 / FastHS-20 / Jolteon-21 | ❇️ $(f_m \cdot \Delta + n \cdot \delta)$ | ⚠️ $O(f_m\cdot n^2 + n^2)$ | same | same |
| Ditto-21 / BoltDumbo-21 | same as above | same as above | ❇️ yes | same |
| RareSync-22 / Lewis-Pye-22 | ⚠️ $O(n \cdot \Delta)$ if $f_m > 0$
$O(n \cdot \delta$) otherwise |
❇️ $O(n^2)$ | no | same |
| Fever-23 | ❇️ $(f_m \cdot \Delta + n \cdot \delta)$ | same as above | same | ⚠️ Required |
| Lumiere | same as above | same as above | same | ❇️ Not required |
