The Latest View on View Synchronization
Authors: Dahlia Malkhi and Oded Naor.
Byzantine consensus protocols that employ a view-by-view paradigm rely on a “Pacemaker” to coordinate among a set of participants—also called nodes—entering and leaving views. A Pacemaker needs to ensure that nodes eventually arrive at a view with an honest leader and spend a sufficient amount of time in overlap in the view to reach a consensus decision. This problem is known as the Byzantine View Synchronization problem.
Steady progress in the practicality of leader-based Byzantine consensus protocols, including the introduction of HotStuff—whose leader protocol incurs only a linear communication cost—shifts the main challenge to keeping the Pacemaker communication complexity low.
This post provides a foundational perspective on the evolution of Pacemaker solutions to the Byzantine View Synchronization problem. Spoiler alert: The theoretical worst-case communication lower bound for reaching a single consensus decision is quadratic, but only this year has this complexity (finally) been achieved; these quadratic Pacemakers are described below.
Background
Many Byzantine consensus protocols for the partial-synchrony setting, and likewise blockchain protocols in a setting with known participants, progress in a view-by-view manner. In each view, one designated node is elected as the leader and proposes a new block of transactions, sends this block proposal to all the other nodes, and collects their votes on its approval. Once the proposed block has enough votes, the leader can continue the protocol and the proposed block is added to the blockchain.
This type of solution gets around the impossibility of reaching consensus in asynchronous networks by waiting for transmissions to become synchronous (aka. global stabilization time or “GST”). After GST, they rely on an honest leader with timely communication with all other honest nodes in the network to drive a consensus decision.
Relying on a good leader to drive progress is based on a “hidden” assumption: All participants are in a view with an honest leader for sufficient time in overlap. Since a node will only vote for a block proposal made by the leader of the view the node is currently in, without this assumption a leader can propose a new block, but it won’t be able to collect enough votes from the honest nodes. The problem of coordinating honest nodes to enter the same view and spend sufficient time in overlap in a view before departing, such that the view has a known honest leader, is the essence of the Byzantine View Synchronization problem.
We proceed to describe an evolution of “Pacemaker” solutions to this problem.
Model and Definition
We focus on systems that may go through a long period of asynchrony—where messages may take arbitrarily long to arrive—until they reach a period of synchrony known as a global stabilization time (GST), after which the network is synchronous and messages arrive within some time-bound. This model is known as “eventually synchronous”.
There are n nodes, up to f < n/3 of which are Byzantine, and the rest of the nodes are honest. The solutions we survey fall into two categories, single-shot and multi-shot (a blockchain). For uniformity, our discussion and complexity measures focus on the single-shot problem.
Intuitively, we think of deterministic protocols that have a view-by-view structure. Each view has a single leader that all the nodes agree on (e.g., by round-robin, or some common source of randomness). Honest nodes run a Pacemaker protocol to progress views (numbered 1,2,3,…).
A view is considered “Coordinated” when all honest nodes are in the same view for a sufficiently long time Δ (dictated by the underlying consensus protocol). The time Δ should allow an honest leader of a Coordinated View enough time in which all the nodes are in the same view (and thus agree on the same leader) to drive the decision process and get all the nodes to vote on a new block proposal. In the Byzantine View Synchronization problem, nodes coordinate entering and leaving views until they arrive at a Coordinated View whose leader is honest. For a blockchain protocol, where new blocks are added continuously to the blockchain, View Synchronization recurs an infinite number of times throughout the run of the protocol: A new leader will propose a new block that will get enough votes, and that’s how the blockchain constantly grows with new blocks.
View Synchronization performance is measured in terms of message complexity and latency. Message complexity is the number of messages (of bounded size) that honest nodes send to each other to reach a single instance of View Synchronization. It counts messages sent starting after the system has become synchronous. Latency is the number of communication rounds it takes. View Synchronization requires repeated Coordinated Views until arriving at one whose leader is honest. The overall cost of reaching View Synchronization depends on the number of consecutive attempted Coordinated Views with Byzantine leaders until a view with an honest leader is entered. Since leaders can be randomly chosen using a common source of randomness, we can discuss the expected and worst-case performance separately. In expectation, with ⅔ honest nodes, it takes a constant number of consecutive Coordinated Views with randomized leader selection to reach a view with an honest leader. In the worst case, it can take up to f consecutive Coordinated Views with Byzantine leaders until an honest leader emerges.
Why is View Synchronization the Bottleneck of Consensus?
There exist deterministic Byzantine consensus protocols, e.g., HotStuff by Yin-Malkhi-Reiter et al., that reach consensus in linear communication complexity once a Synchronized View is reached. Indeed, HotStuff was the first consensus protocol that explicitly separated the core consensus algorithm from a component that instructs each node to advance views. They named this component a Pacemaker (without providing a concrete implementation), and its job was only to achieve View Synchronization. HotStuff reaches consensus in a Synchronized View in O(1) latency and O(n) message complexity. After GST, O(f) Coordinated Views may be needed in the worst case to drive a consensus decision, hence, HotStuff could incur O(n²) communication in total (O(n) messages in each of the O(f) Coordinated Views).
This matches a known lower bound for the message complexity of any deterministic Byzantine consensus protocol discovered by Dolev and Reischuk in 1980. This bound stipulates that every deterministic solution has executions that incur message complexity O(n²) (even during perfectly synchronous settings).
However, this is not the end of the story.
HotStuff incurs only a linear communication cost once a Synchronized View is reached, but a Pacemaker incurs additional communication cost in coordinating entering and leaving views to arrive at such a Synchronized View.
As a straw-man solution, nodes could coordinate entering a view via an all-to-all broadcast based on Bracha’s reliable broadcast. Briefly, a node in view r performs the following actions:
- If there is no progress, it broadcasts
(READY,r+1). - If it receives
(READY,r+1)broadcasts from f+1 other nodes, it broadcasts(READY,r+1). - If it receives
(READY,r+1)broadcasts from 2f+1 other nodes, it enters view r+1.
Unfortunately, with this solution, an unlucky succession of O(f) views with faulty leaders incurs O(n³) communication. As a result, plugging this naive Pacemaker in a consensus solution (e.g., HotStuff) incurs an overall cubic communication complexity.
Improving the complexity of View Synchronization would improve the overall consensus complexity, and in particular, any view synchronization solution that has O(n²) complexity would therefore prove Dolev-Reischuk lower bound tight in the partial synchrony setting. This will also close a gap from the synchronous model, in which Momose and Ren already showed the bound tight.
We note that there is a known O(n) latency lower bound on the number of views that every deterministic solution might suffer, introduced by Dolev and Strong in 1983. All the Pacemakers described below achieve this latency, but most of them have a lower expected latency. Most of the Pacemakers described below have a lower expected latency.
Pacemakers
The Byzantine View Synchronization problem was formally defined first in Cogsworth. In later works, the problem was generalized for single-shot consensus and blockchains. Before that, consensus protocols did not have explicit Pacemaker algorithms, and, rather, implicitly used techniques to get nodes synchronized to the same view.
For example, PBFT uses exponential back-off: If a node doesn’t make progress in a view in time t, it moves to the next view and spends 2t time there. This process continues until the consensus protocol progresses to a decision. Doubling the time in each view guarantees eventually reaching a view in which all the honest nodes overlap for at least Δ (and it works even if Δ is unknown). This is a simple approach, but the downside is that the number of attempted views to reach View Synchronization is unbounded—even after GST and without any faults—and therefore latency and communication costs are unbounded.
In later protocols, nodes communicate to synchronize views. The table below lists known solutions and their latency and message complexity (for both the expected and worst case) after GST. The meaning of the parameter 𝛿 is explained below.
| Pacemaker Protocol | Expected Latency | Worst Case Latency | Expected Message Complexity | Worst Case Message Complexity |
| Bracha based / FastSync | O(1) | O(n) | O(n²) | O(n³) |
| Cogsworth | O(1) | O(n)
in max{Δ, f·𝛿} units |
O(n) with benign faults
O(n²) with Byzantine faults |
O(n²) with benign faults
O(n³) with Byzantine faults |
| Naor-Keidar | O(1) | O(n)
in max{Δ, f·𝛿} units |
O(n) | O(n³) |
| RareSync / Lewis-Pye | O(n) | O(n) | O(n²) | O(n²) |
As mentioned in the straw-man approach above, a naive solution of View Synchronization is to use a broadcast protocol based on Bracha’s reliable broadcast. This is a leaderless protocol in which there is an all-to-all O(n²) communication step to synchronize each view:
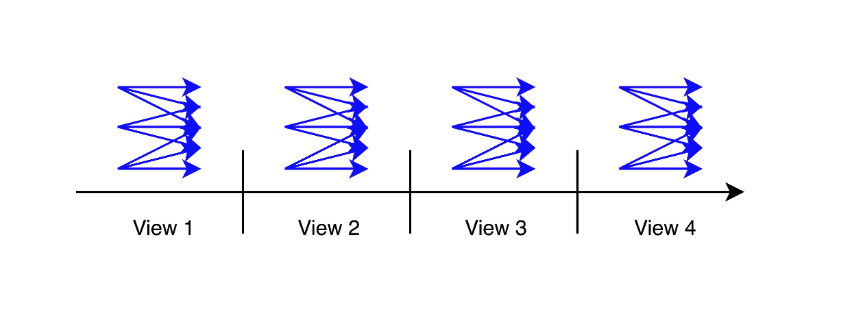
After GST, this protocol coordinates all nodes to enter a new Coordinated View within constant latency: Let r be the highest view that an honest node wants to enter. Then f+1 honest nodes must have entered r−1 and sent READY broadcasts for r. After they expire view r−1, it takes one network latency for f+1 READY broadcasts to spread and another latency for READY broadcasts by f additional honest nodes, until everyone enters r. There are potentially f Byzantine leaders in succession in the worst case, hence the worst case latency is O(f)=O(n), matching the latency lower bound, and O(n³) worst case message complexity, which is higher than the communication lower bound. In the expected case, it takes a constant number of Coordinated Views until there is an honest leader, leading to O(1) expected latency and O(n²) expected message complexity.
FastSync is similarly based on Bracha broadcast, but has bounded memory and tolerates message loss before GST.
Cogsworth improves the communication complexity and latency in the expected case for runs with benign nodes. In Cogsworth, when nodes want to move to the next view, they send a message only to the next view’s leader. The leader collects the messages from the nodes, and once it receives enough messages, it combines them into a threshold signature and sends it to the nodes. This all-to-leader, leader-to-all communication pattern is similar to the one used in HotStuff:
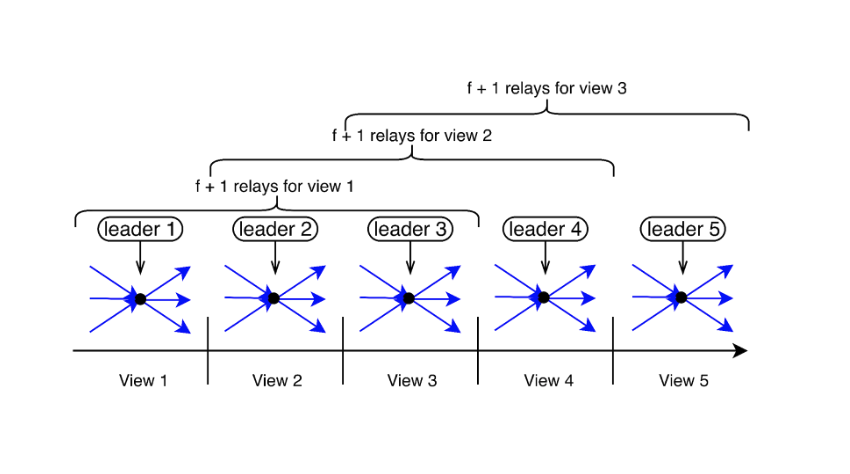 Cogsworth operates in two phases similar to Bracha’s protocol, routing messages through leaders in lieu of broadcast. Briefly, a node in view r performs the following actions:
Cogsworth operates in two phases similar to Bracha’s protocol, routing messages through leaders in lieu of broadcast. Briefly, a node in view r performs the following actions:
- If there is no progress, it sends the leader of view r+1 a message
(WISH,r+1). - A leader collects f+1
(WISH,r+1)messages and relays an aggregate to the nodes. - If a node receives a
WISHaggregate from any leader, it responds with(READY,r+1). - Otherwise, if a node wishes to enter view r+1 but does not receive a
WISHaggregate within a timeout period 𝛿,, it repeats the above with fallback leaders of views r+2,…,r+f+1, one by one, until there is progress. - A leader collects 2f+1
(READY,r+1)messages and broadcasts aREADYaggregate to the nodes. - If a node receives a
READYaggregate from any leader, it enters view r+1. - Otherwise, if a node holds a
WISHaggregate but does not receive aREADYaggregate within a timeout period 𝛿,, it forwards theWISHaggregate to fallback leaders of views r+2,…,r+f+1, one by one, to collectREADYresponses, until there is progress.
Like Bracha, this scheme requires 2f+1 nodes to send a READY message to enter a view. This ensures that if an honest node wishes to enter view r+1, then f+1 honest nodes already entered view r. If there is no progress, these f+1 honest nodes will expire within a constant latency and be ready to enter r+1. However, unlike Bracha, the leader is responsible for relaying all transmissions, hence a faulty leader might prevent the proper spreading of messages among honest nodes. The trick in Cogsworth is utilizing f+1 consecutive leaders as fallback relayers, attempting leaders one at a time—each after a timeout—until there is progress. This ensures that at least one of the relayers is an honest node that will correctly execute the protocol.
Cogsworth attempts an expected constant number of fallback leaders, hence its message complexity to reach a Coordinated View in the expected case is O(n) and the latency is O(1) in runs with benign faults (a benign fault is when a node crashes or stops sending messages). In expectation, a constant number of Coordinated Views are attempted to reach a view with an honest leader, hence the expected latency after GST is constant and the overall expected communication quadratic. However, even a single Byzantine node can trigger f+1 consecutive leaders to “relay” WISH aggregates (in false fallbacks). Therefore, the expected communication cost per Coordinated View in face of Byzantine failures is as bad as the Bracha-based protocol, O(n²).
The worst case latency of Cogsworth happens when there is a cascade of O(n) Coordinated Views with faulty leaders, each incurring a latency of max{f · 𝛿, Δ} due to view synchronization. In practice, 𝛿 can be set to be much lower than Δ, the worst case network delay, without affecting the protocol’s correctness or liveness. However, suboptimal expected message complexity can be caused if 𝛿 is lower than the actual round trip time of sending a message to the relays and back.
The Naor-Keidar protocol improves Cogsworth’s performance and achieves O(n) message complexity and O(1) latency in the expected case also in runs with Byzantine faults. It uses the same communication pattern as Cogsworth but adds another field to WISH messages that prevents a Byzantine leader from inflicting O(n²) communication. Adding this field requires adding another phase of communication after nodes enter views to ensure that at least f+1 honest nodes have entered; the details are omitted here. As explained above, these f+1 honest nodes are the threshold needed to later initiate the protocol to advance to the next view.
Two works published in 2022, RareSync and the Lewis-Pye protocol, improve the worst-case performance to (finally) arrive at an optimal consensus protocol. Both use a similar approach, which is remarkably simple and elegant. It bundles consecutive views into epochs, where each epoch consists of f+1 consecutive views. Nodes employ a Bracha-like all-to-all coordination protocol in the first view of each epoch, and then they advance through the rest of the views in the same epoch using timeouts if there is no progress in the underlying consensus protocol:
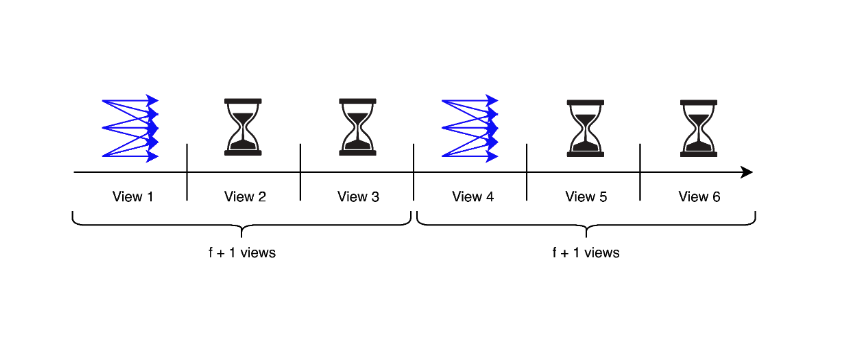
The worst-case message complexity is O(n²) messages per View Synchronization, with O(n) latency: Nodes send O(n²) messages per epoch and each epoch takes O(n) view timeouts.
Because nodes synchronize only at the first view of each epoch, they may need to advance through f+1 un-Coordinated Views after GST to reach the synchronization step. Therefore, the downside is that the expected message complexity and latency are identical to the worst case, hence the expected case performance is worse than previous solutions. It remains an open question whether there is a protocol with O(n²) message complexity and O(n) latency in the worst case (matching the known lower bounds), but O(n) complexity and O(1) latency in the expected case.
The difference between the two works is that the Lewis-Pye protocol solves the problem for multi-shot (blockchain) setting while RareSync is for single-shot. Lewis-Pye is also optimistically responsive, meaning that in good periods of execution the protocol works at network speed.
These last two protocols answer in the affirmative that the celebrated Dolev-Reischuk lower bound is tight in the eventual synchronous model.
Acknowledgments: We thank Ben Fisch, Rachid Guerraoui, and Andrew Lewis-Pye for their comments that helped improve this post.
Reading list
- “Cogsworth: Byzantine View Synchronization”. Naor, Baudet, Malkhi, and Spiegelman (2019).
- “Expected linear round synchronization: The missing link for linear Byzantine SMR”. Naor and Keidar (2020).
- “Making Byzantine Consensus Live”. Manuel, Chockler, and Gotsman (2020).
- “Liveness and Latency of Byzantine State-Machine Replication”. Manuel, Chockler, and Gotsman (2022).
- “Byzantine Consensus is Θ(n²): The Dolev-Reischuk Bound is Tight even in Partial Synchrony!”. Pierre, Dzulfikar, Gilbert, Gramoli, Guerraoui, Komatovic, and Vidigueira (2022).
- “Quadratic worst-case message complexity for State Machine Replication in the partial synchrony model”. Lewis-Pye (2022).
