BFT on a DAG
Synopsis
Emerging Proof-of-Stake blockchains achieve high transaction throughput by spreading transactions reliably as fast as the network can carry them and accumulating them in a DAG. Then, participants interpret their DAG locally without exchanging more messages and determine a total ordering of accumulated transactions.
This post explores a simple and efficient DAG-based BFT Consensus ordering method – quite possibly the simplest way to embed BFT in a DAG. It operates in a view-by-view manner that guarantees that when the network is stable, only two broadcast latencies are required to reach a consensus decision on all the transactions that have accumulated in the DAG. Importantly, the DAG never has to wait for Consensus protocol steps/timers to add transactions.
Introduction
Recent DAG-based systems (see suggested reading below) demonstrate excellent performance by separating the responsibility of spreading messages reliably and with causal ordering from the Consensus ordering logic:
- A DAG transport is responsible for reliably spreading yet-unconfirmed transactions. It regulates communication and optimizes throughput, but it tracks only causal ordering in the form of a DAG (Direct Acyclic Graph).
- A BFT (Byzantine Fault Tolerant) Consensus protocol is responsible for forming agreement on a serial commit ordering of transactions. Each party utilizes its local copy of the DAG to independently extract the common ordering of transactions from the DAG structure.
The advent of building Consensus over a DAG transport is that each message in the DAG spreads useful payloads (transactions or transaction references). Each time a party sends a message with transactions, it also contributes at no cost to forming the total ordering of committed transactions. Parties can continue sending messages and the DAG keeps growing even when the Consensus protocol is stalled, e.g., when a Consensus leader is faulty, and later commit the messages accumulated in the DAG. Additionally, the non-equivocating property of DAG messages and the causality information they carry can remove much of the complexity in the design of Consensus protocols.
This post explores a simple method to build Consensus over a reliable and causally ordered communication transport. The method borrows from and builds on many previous works (see suggested reading below). However, uniquely it provides a minimalist and purist approach emphasizing the following key tenets:
- Zero DAG delay. Our approach provides a clean separation of Consensus ordering logic from the DAG transport. Consensus uses the DAG solely as a “smart mempool” to spread transactions and meta-information. By comparison, to get from the Consensus method described here to just one (small) part of a Consensus protocol like Bullshark, you would need to stipulate a layered DAG structure, add a requisite number of predecessors on each DAG message, and condition each DAG transmission on Consensus steps/timers.
- Simple. Our method is quite possibly the simplest DAG-based protocol for the partial synchrony model. In a nutshell, it is a view-by-view protocol: the leader of a view broadcasts into the DAG a proposal that becomes committed when it is causally followed by enough votes in the DAG. Advancing to the next view is enabled by either a commit or by complaints which are broadcast into the DAG. That’s the entire protocol!
- Partial synchrony. The solution guarantees that when the network is stable, only two broadcast latencies are required to reach a Consensus decision. An ordering decision commits in a batch all the transactions that have accumulated in the DAG.
This post is meant for pedagogical purposes, not as a full-fledged BFT system design: we wanted a simple, minimalist approach to serve as an algorithmic foundation on which constructions like Fino (the subject of a future post) can be built and proven correct. Like most advances, the method described here stands on the shoulders of a long history of works (see suggested reading below). The main takeaway on the field is that Consensus on a DAG can be simple and highly performant at the same time.
What is DAG-based BFT?
In a DAG-based BFT protocol, parties store messages delivered via reliable and causally ordered broadcast in a local graph. When a message is inserted into the local DAG, it has the following guarantees:
- Reliability: there are copies of the message stored on sufficiently many participants, such that eventually, all honest parties can download it
- Non-equivocation: messages by each party are numbered. If a party delivers some message as the k’th from a particular sender, then the message is authenticated by its sender and other parties deliver the same message as the sender k’th message.
- Causal ordering: the message carries explicit references to messages which the sender has previously delivered (including its own). Predecessors are delivered locally before the message is delivered.
Note that the DAGs at different parties may be slightly different at any moment in time. This is inevitable in a distributed system due to message scheduling. However, a DAG-based Consensus protocol allows each participant to interpret its local DAG, reaching an autonomous conclusion that forms total ordering. Reliability, Non-equivocation and Causality, make the design of such protocols extremely simple as we shall see below.
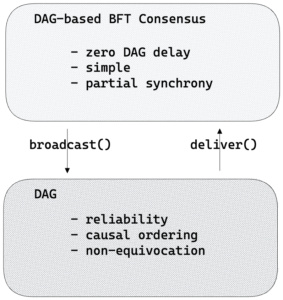
The lifetime of a DAG message. A DAG transport exposes two basic API’s, broadcast() and deliver().
- Broadcast.
broadcast()is an asynchronous API for a party to present payload for the DAG transport to be transmitted to all other parties. The main use of DAG messages in a DAG-based Consensus protocol is to pack meta-information on transactions into a block and present the block for broadcast. The DAG transport adds references to previously delivered messages, and broadcasts a message carrying the block and the causal references to all parties. - Deliver. When another party receives the message carrying the block, it checks whether it needs to retrieve a copy of any of the transactions in the block and in causally preceding messages. Once it obtains a proof-of-availability of all transactions in the block and its causal past, it can acknowledge it. A party’s upcall
deliver(m)is triggered when sufficiently many acknowledgments for it are gathered, guaranteeing that the message itself, the transactions it refers to, and its entire causal past maintain Reliability, Non-equivocation and Causal-ordering.
Implementing a DAG. There are various ways to implement reliable and causally-ordered broadcast among n=3F+1 parties, at most F of which are presumed Byzantine faulty and the rest are honest.
- Echoing. The key mechanism for reliability and non-equivocation is for parties to echo a digest of the first message they receive from a sender with a particular index. There are two commonly known ways to echo, one is all-to-all broadcast over authenticated point-to-point channels a la Bracha Broadcast; the other is converge-cast with cryptographic signatures a la Rampart. In either case, echoing can be streamlined so the amortized per-message communication is linear, which is anyway the minimum necessary to spread the message.
- Layering. Transports are often constructed in a layer-by-layer regime. In this regime, each sender is allowed one message per layer, and a message may refer only to messages in the layer preceding it. Layering is done so as to regulate transmissions and saturate network capacity, and has been demonstrated to be highly effective by various projects, including Blockmania, Aleph, and Narwhal. We reiterate that the Consensus protocol described here does not require a layered structure.
Fino’s DAG-based BFT consensus
We demonstrate the utility of a DAG through Fino’s core, a BFT Consensus ordering protocol embedding designed for the partial synchrony model, solving Consensus among n=3F+1 parties of which F may be Byzantine.
Given the strong guarantees of a DAG transport, the embedding is quite simple, quite possibly the simplest DAG-based Consensus solution for the partial synchrony model. It operates in one-phase, and is completely out of the critical path of DAG transaction spreading.
Briefly, the method works as follows:
- Views. The protocol operates in a view-by-view manner. Each view is numbered, as in
view(r), and has a designated leader known to everyone. Each view consists of proposals, votes, and complaints embedded inside the DAG. - Proposals. When a leader enters
view(r)it broadcastsproposal(r). A proposal is just like any message in the DAG, it contains transaction meta-information and causal predecessors. Each proposal is interpreted to include a batch: all transactions in its causal past, including those directly included in the proposal message, that haven’t been included in a preceding proposal already. - Votes. Other parties in
view(r), after deliveringproposal(r), broadcast avote(r). A vote is just like any message in the DAG. It is interpreted as a vote by causally followingproposal(r)inview(r). - Complaints. To indicate that
view(r)is not progressing, parties broadcastcomplaint(r). After complaining, a party cannot vote inview(r). Note that to guarantee progress during steady state, complaints are emitted only after allowing a leader sufficient time to propose and for votes to arrive. - Commit. A commit happens at
view(r)if there are F+1 votes for the leader proposal, - Next view. Entering
view(r+1)is enabled either by a commit or by 2F+1 complaints.
Importantly, proposals, votes, and complaints are injected into the DAG at any time, independent of layers. Likewise, protocol views do NOT correspond to DAG layers. This property is a key tenet of the DAG/Consensus separation, allowing the DAG to continue spreading messages with Consensus completely out of the critical path.
The solution is so simple due to the DAG properties: Consensus logic does not need to consider leader equivocation, because DAG prevents it. A leader does not need to justify its proposal because it is inherently justified through the proposal’s causal history within the DAG. Safety of a commit in a view is gated by advancing to the next view after F+1 votes or 2F+1 complaints, guaranteeing intersection with F+1 commit votes.
The full protocol is described in pseudo-code below in Pseudo-Code. A step by step scenario walkthrough is provided next.
Scenario-by-scenario walkthrough
Happy path scenario.
Every party enters view(r) by causally following a commit in view(r-1) or complaint(r-1) messages by 2F+1. Each view(r) has a pre-designated leader, denoted leader(r), which is known to everyone.
The first view(r) message by the leader is interpreted as proposal(r). The proposal implicitly contains a batch: all the transactions that causally precede the proposal (including itself) which haven’t been included in a preceding batch.
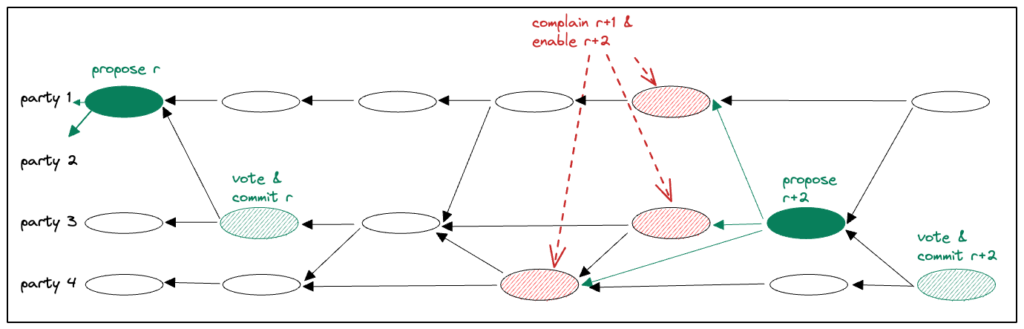
In Figure 1 below, leader(r) is party 1 and its first message in view(r) is denoted with a full green oval, indicating it is proposal(r).
After a party delivers proposal(r), its first message following the proposal is interpreted as vote(r). A proposal that has a quorum of F+1 votes is considered committed.
In Figure 1 below, party 3 votes for proposal(r), denoted with a striped green oval. proposal(r) now has the required quorum of F+1 votes (including the leader’s implicit vote), and it becomes committed. The batch of transactions in the causal past of proposal(r) are appended to the Consensus sequence of committed transactions.
When a party sees F+1 votes in view(r) it enters view(r+1).
Scenario with a faulty leader.
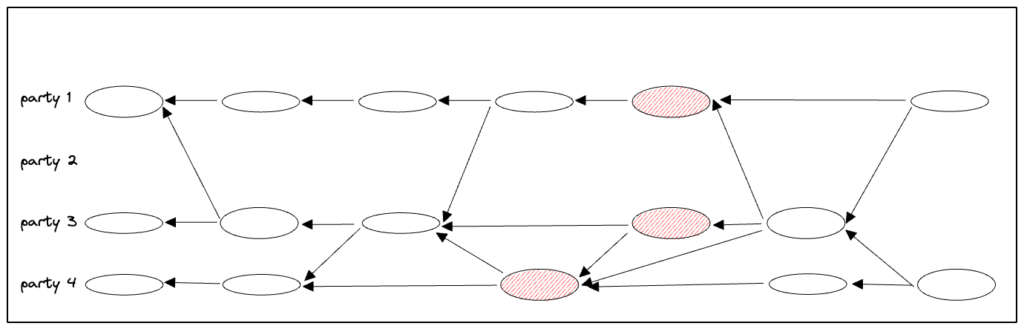
If the leader of a view is faulty or disconnected, parties will eventually time out and broadcast a complaint message. When a party sees 2F+1 complaints about a view, it enters the next view.
In Figure 1 above, the first view view(r) proceeds normally. However, no message marked view(r+1) by party 2 who is leader(r+1) arrives, showing as a missing ovals. No worries! As depicted, DAG transmissions continue, unaffected by the leader’s failure. Hence, faulty views have utility in spreading transactions. Eventually, parties 1, 3, 4 complain about view(r+1), showing as striped red ovals. After 2F+1 complaints are collected, the leader of view(r+2) posts a message that is taken as proposal(r+2). The proposal’s batch contains all messages that have accumulated in its causal history, all contributing to throughput.
Scenario with a slow leader. A slightly more complex scenario is depicted in Figure 2 below. This scenario is the same as above but with leader(r+1) actually issuing proposal(r+1), denoted as a full red oval, which is simply too slow to arrive at parties 1, 3 and 4. These parties complain about a view failure, enabling view(r+2) to start without committing proposal(r+1). However, proposal(r+2) causally follows proposal(r+1) and when proposal(r+2) commits, it indirectly commits proposal(r+1). First the batch in the causal history of proposal(r+1)is appended to the Consensus sequence of committed transactions, second the remaining causal history of proposal(r+2).
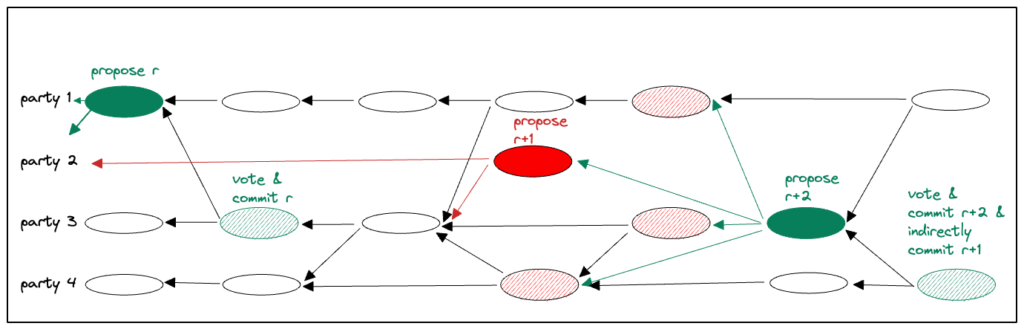
view(r+1) being indirectly committed in view(r+2).In pseudo-code
Messages are delivered in deliver(m) carrying a sender’s payload and additional meta information that can be inspected upon reception:
- m.sender, the sender identity - m.index, a delivery index from the sender - m.payload, contents such as transaction(s) and BFT protocol meta-information piggybacked on transmissions - m.predecessors, references to messages sender has delivered from other parties, including itself
Party p performs the following operations for view(r):
1. Entering a view. A party enters view(r) if the DAG satisfies one of the following two conditions: (i) A commit of proposal(r-1) happens (ii) 2F+1 complaint(r-1) messages are delivered Initially, view 1 is entered. 2. Proposing. A message in the DAG is proposal(r) if it is the first broadcast of leader(r) in view(r). 3. Voting. A message in the DAG is vote(r) for the leader’s proposal(r) if: (i) It is the first broadcast of party p in view(r) that causally follows proposal(r) or it is proposal(r) itself (ii) It does not follow a complaint(r) message by p 4. Committing. A proposal(r) becomes committed if there are F+1 vote(r) messages in the DAG. Upon a commit of proposal(r), a party disarms the view(r) timer. 4.1. Ordering commits. If proposal(r) commits, messages are appended to the committed sequence as follows. First, among proposal(r)'s causal predecessors, the highest proposal(s) is (recursively) ordered. After it, remaining causal predecessors of proposal(r) including the proposal itself, which have not yet been ordered, are appended to the Consensus sequence of committed transactions. (Within this batch, ordering can be done using any deterministic rule to linearize the partial ordering into a total ordering.) 5. Expiring the view timer. If the view(r) timer expires, a party broadcasts complaint(r).
Analysis
The method presented above is minimally integrated into the DAG, simply interpreting broadcasts carrying blocks of transaction-references, and presenting view-complaints for broadcast as needed. Importantly, at no time is the DAG broadcast slowed down by or waits for the Consensus protocol.
The reliability and causality properties of the DAG makes arguing about correctness very easy, though a formal proof of correctness is beyond the scope of this post.
Safety (sketch). If ever proposal(r) becomes committed, then it is in the causal past of F+1 parties that voted for it. A proposal of any higher view must refer (directly or indirectly) to F+1 vote(r) messages, or to 2F+1 complaint(r) messages of which one follows a proposal(r). In either case, a commit in such a future view causally follows a vote for proposal(r), hence, it (re-)commits it.
Conversely, when proposal(r) commits, it may cause a proposal in a lower view, proposal(s), where s < r, to become committed for the first time. Safety holds because future commits will order proposal(r) and its causal past recursively in the same manner.
Liveness (sketch) during periods of synchrony. After GST (Global Stabilization Time), i.e., after communication has become synchronous, views are inherently synchronized through the reliable DAG broadcast. For let Δ be an upper bound on DAG broadcast after GST. Once a view(r) with an honest leader is entered by the first honest party, within Δ, all the messages seen by party p are delivered by both the leader and all other honest parties. Hence, within Δ, all honest parties enter view(r) as well.
Within additional 2Δ, the view(r) proposal and votes from all honest parties are spread to everyone. So long as view timers are set to be at least 3Δ, a future view does not preempt a current view’s commit. For in order to start a future view, its leader must collect either F+1 vote(r) messages, hence commit proposal(r); or 2F+1 complaint(r) expiration messages, which is impossible as argued above.
We now remark about communication complexity during steady state, when a leader is honest and communication with it is synchronous:
- DAG message cost: In order for DAG messages to be delivered reliably, it must implement reliable broadcast. This incurs either a quadratic number of messages carried over authenticated channels, or a quadratic number of signature verifications, per broadcast. In either case, the quadratic cost may be amortized by pipelining, driving it in practice to (almost) linear per message.
- Commit message cost: The protocol sends O(n) broadcast messages, a proposal and votes, per decision. A decision commits the causal history of the proposal, consisting of (at least) a linear number of messages. Moreover, each message may carry multiple transactions in its payload. As a result, in practice the commit cost is amortized over many transactions.
- Commit latency: The commit latency in terms of DAG messages is 2, one proposal followed by votes.
Related DAG-based solutions
Early DAG based consensus systems focused on data-center replication, e.g., Isis, Psync, Trans, Total and Transis. Total and ToTo are pre- blockchain era, pure-DAG total ordering protocols for the asynchronous model. These pure DAG protocols are designed without regulating DAG layers, and without injecting external common coin-tosses to cope with asynchrony. As a result, they are both quite complex and their convergence slow.
An intense debate over the usefulness of CATOCS (Causal and Totally Ordered Communication) from that era is documented in a position paper by Cheriton and Skeen [CATOCS, 1993], followed by Birman’s [response 1 to CATOCS, 1994] and Van Renesse’s [response 2 to CATOCS, 1994].
Recent interest in scaling blockchains rekindled interest in DAG-based protocols. Several blockchain projects are being built using DAG-based Consensus protocols high-throughput, including Swirlds hashgraph, Blockmania, Aleph, Narwhal & Tusk, DAG-rider, and Bullshark.
Swirlds Hashgraph is the only blockchain era, pure-DAG solution to our knowledge. It makes use of bits within messages as pseudo-random coin-tosses in order to drive randomized Consensus.
Narwhal is a DAG transport that has a layer-by-layer structure, each layer having at most one message per sender and referring to 2F+1 messages in the preceding layer. A similarly layered DAG construction appears earlier in Aleph.
Narwhal-HS is a BFT Consensus protocol based on HotStuff for the partial synchrony model, in which Narwhal is used as a “mempool”. In order to drive Consensus decisions, Narwhal-HS adds messages outside Narwhal, using the DAG only for spreading transactions.
DAG-Rider and Tusk build randomized BFT Consensus for the asynchronous model “riding” on Narwhal, These protocols are “zero message overhead” over the DAG, not exchanging any messages outside the Narwhal protocol. DAG-Rider (Tusk) is structured with purpose-built DAG layers grouped into “waves” of 4 (2) layers each.
Bullshark builds Byzantine Consensus riding on Narwhal for the partial synchrony model. It is designed with 8-layer waves driving commit, each layer purpose-built to serve a different step in the protocol. Bullshark is a “zero message overhead” protocol over the DAG, but advancing layers may be delayed by consensus timers.
Acknowledgement: Many thanks to Lefteris Kokoris-Kogias for pointing out practical details about Narwhal and Bullshark, that helped improve this post.
Suggested reading
Pre-blockchains era:
- “Exploiting Virtual Synchrony in Distributed Systems”, Birman and Joseph, 1987. [Isis]
- “Asynchronous Byzantine Agreement Protocols”, Bracha, 1987. [Bracha Broadcast]
- “Preserving and Using Context Information in Interprocess Communication”, Peterson, Buchholz and Schlichting, 1989. [Psync]
- “Broadcast Protocols for Distributed Systems”, Melliar-Smith, Moser and Agrawala, 1990. [Trans and Total]
- “Total Ordering Algorithms”, Moser, Melliar-Smith and Agrawala, 1991. [Total (short version)]
- “Byzantine-resilient Total Ordering Algorithms”, Moser and Melliar Smith, 1999. [Total]
- “Transis: A Communication System for High Availability”, Amir, Dolev, Kramer, Malkhi, 1992. [Transis]
- “Early Delivery Totally Ordered Multicast in Asynchronous Environments”, Dolev, Kramer and Malki, 1993. [ToTo]
- “Understanding the Limitations of Causally and Totally Ordered Communication”, Cheriton and Skeen, 1993. [CATOCS]
- “Why Bother with CATOCS?”, Van Renesse, 1994. [Response 1 to CATOCS]
- “A Response to Cheriton and Skeen’s Criticism of Causal and Totally Ordered Communication”, Birman, 1994. [Response 2 to CATOCS]
- “Secure Agreement Protocols: Reliable and Atomic Group Multicast in Rampart”, Reiter, 1994. [Rampart].
Blockchain era:
- “The Swirlds Hashgraph Consensus Algorithm: Fair, Fast, Byzantine Fault Tolerance”, Baird, 2016. [Swirlds Hashgraph]
- “Blockmania: from Block DAGs to Consensus”, Danezis and Hrycyszyn, 2018. [Blockmania].
- “Aleph: Efficient Atomic Broadcast in Asynchronous Networks with Byzantine Nodes”, Gągol, Leśniak, Straszak, and Świętek, 2019. [Aleph]
- “Narwhal and Tusk: A DAG-based Mempool and Efficient BFT Consensus”, Danezis, Kokoris-Kogias, Sonnino, and Spiegelman, 2021. [Narwhal and Tusk]
- “All You Need is DAG”, Keidar, Kokoris-Kogias, Naor, and Spiegelman, 2021. [DAG-rider]
- “Bullshark: DAG BFT Protocols Made Practical”, Spiegelman, Giridharan, Sonnino, and Kokoris-Kogias, 2022. [Bullshark]
- “MEV protection on a DAG”, Malkhi and Szalachowski, 2022. [MEV Protection on DAG]
